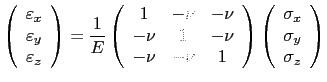Ecuaciones de Lamé

Si las ecuaciones de (4.21), correspondientes a las tensiones normales, se expresan en forma matricial, se obtiene

$\displaystyle \left( \begin{array}{c} \varepsilon_x \\ \varepsilon_y \\ \... ...begin{array}{c} \sigma_x \\ \sigma_y \\ \sigma_z \\ \end{array} \right)$ (4.22)

Expresando las tensiones en función de las deformaciones, invirtiendo la matriz de constantes elásticas, se obtiene

$\displaystyle \left( \begin{array}{c} \sigma_x \\ \sigma_y \\ \sigma_z \\... ... \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \end{array} \right)$ (4.23)

Las tensiones tangenciales se pueden expresar en función de las deformaciones tangenciales, ecuación (4.21), como sigue

\begin{displaymath}\begin{array}{c} \tau_{xy} = G\gamma_{xy} \vspace{0.15cm}\\ ... ..._{xz} \vspace{0.15cm}\\ \tau_{yz} = G\gamma_{yz} \end{array}\end{displaymath} (4.24)

Haciendo 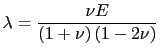$ \lambda=\displaystyle\frac{\nu E}{\left(1+\nu\right)\left(1-2\nu\right)}$, y conociéndose que 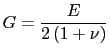$ G=\displaystyle\frac{E}{2\left(1+\nu\right)}$, las ecuaciones (4.23) y (4.24) se pueden expresar como

\begin{displaymath}\begin{array}{ccc} \sigma_x &=& \lambda \hspace{1mm} e + 2G\... ...z} \vspace{0.15cm} \\ \tau_{yz} &=& G\gamma_{yz} \end{array}\end{displaymath} (4.25)

siendo $ e=\varepsilon_x+\varepsilon_y+\varepsilon_z$. Las ecuaciones (4.25) constituyen las llamadas ecuaciones de Lamé, y expresan las tensiones en función de las deformaciones.

En caso de tensión plana, las ecuaciones de Lamé se simplifican. Si se trabaja en el plano $ xy$, las ecuaciones son

\begin{displaymath}\begin{array}{ccc} \sigma_x &=& \displaystyle\frac{E}{1-\nu^... ...vspace{0.25cm} \\ \tau_{xy} &=& G\gamma_{xy} \\ \end{array}\end{displaymath} (4.26)