Tensión plana

Un sólido está sometido a tensión plana si todas las componentes de la tensión se encuentran en un mismo plano. Si el plano considerado es el $ xy$, se verifica que $ \sigma_z=\tau_{xz}=\tau_{yz}=0$, y el tensor de tensiones es

$\displaystyle \boldsymbol{\sigma}= \left( \begin{array}{cc} \sigma_x & \tau_{xy}\\ \tau_{xy} & \sigma_y \\ \end{array} \right)$ (3.43)

Mediante la fórmula de Cauchy en forma compacta

$\displaystyle \textbf{t}^\textbf{n}=\boldsymbol{\sigma}\textbf{n}$    

es posible conocer las componentes del vector tensión en un punto $ P$ respecto a cualquier plano cuya normal n forme un ángulo $ \theta$ con el eje $ x$, tal y como se muestra en la Figura 3.13.

Figura 3.13: Componentes intrínsecas del vector tensión en un punto respecto a un plano de normal $ \overrightarrow{n}$
Image 13-Tensiones

La fórmula de Cauchy en forma expandida es

$\displaystyle \left( \begin{array}{c} t_x^{n} \vspace{0.1cm}\\ t_y^{n} \vsp... ...m}\\ \text{ sen}\hspace{0.05cm}\theta \vspace{0.1cm}\\ \end{array} \right)$ (3.44)

Las componentes globales del vector tensión son

\begin{displaymath}\begin{array}{c} t_x^{n}= \sigma_x \cos \theta +\tau_{xy} \t... ...\theta + \sigma_y \text{ sen}\hspace{0.05cm}\theta \end{array}\end{displaymath} (3.45)

La componente intrínseca normal $ \sigma $ es


$\displaystyle \sigma$ $\displaystyle =$ $\displaystyle \textbf{n}^{\text{T}} \textbf{t}^\textbf{n} =$  
  $\displaystyle =$ $\displaystyle \left( \begin{array}{cc} \cos \theta & \text{ sen}\hspace{0.0... ...os \theta + \sigma_y \text{ sen}\hspace{0.05cm}\theta \end{array} \right) =$ (3.46)
  $\displaystyle =$ $\displaystyle \sigma_x \cos^2 \theta +\sigma_y$    sen$\displaystyle ^2\hspace{0.05cm}\theta +2 \tau_{xy}$ sen$\displaystyle \hspace{0.05cm}\theta \cos \theta$  

y la componente intrínseca tangencial $ \tau$


$\displaystyle \tau$ $\displaystyle =$ $\displaystyle \textbf{t}^$T$\displaystyle \textbf{t}^\textbf{n} =$  
  $\displaystyle =$ $\displaystyle \left( \begin{array}{cc} -\text{ sen}\hspace{0.05cm}\theta & ... ... \theta + \sigma_y \text{ sen}\hspace{0.05cm}\theta \end{array} \right) =$ (3.47)
  $\displaystyle =$ $\displaystyle -\sigma_x \cos \theta$    sen$\displaystyle \hspace{0.05cm} \theta+\sigma_y \cos \theta$    sen$\displaystyle \hspace{0.05cm} \theta - \tau_{xy}$ sen$\displaystyle ^2\hspace{0.05cm} \theta + \tau_{xy}\cos^2 \theta$  

siendo

$\displaystyle \textbf{t}= \left( \begin{array}{cc} \cos\left(90+\theta\right) & \cos \theta \end{array} \right)^$T$\displaystyle = \left( \begin{array}{cc} -\text{sen}\hspace{0.05cm}\theta & \cos \theta \end{array} \right)^$T    

Mediante las siguientes relaciones trigonométricas


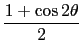$\displaystyle \cos^2 \theta$ $\displaystyle =$ $\displaystyle \displaystyle\frac{1+\cos 2\theta}{2}$  
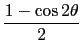$\displaystyle \sen^2 \theta$ $\displaystyle =$ $\displaystyle \displaystyle\frac{1-\cos 2\theta}{2}$  
$\displaystyle \sen 2 \theta$ $\displaystyle =$ $\displaystyle 2 \sen \theta \cos\theta$  
$\displaystyle \cos 2 \theta$ $\displaystyle =$ $\displaystyle \cos^2\theta - \sen^2 \theta$  

las componentes intrínsecas normal y tangencial se pueden expresar como


$\displaystyle \sigma$ $\displaystyle =$ $\displaystyle \displaystyle\frac{\sigma_x+\sigma_y}{2}+\displaystyle\frac{\sigma_x-\sigma_y}{2} \cos 2\theta+\tau_{xy} \sen 2\theta$ (3.48)
$\displaystyle \tau$ $\displaystyle =$ $\displaystyle -\displaystyle\frac{\sigma_x-\sigma_y}{2} \sen 2\theta+ \tau_{xy} \cos 2\theta$ (3.49)

Dejando a un mismo lado de la igualdad los coeficientes multiplicados por funciones trigonométricas, las ecuaciones (3.48) y (3.49) quedan como


$\displaystyle \sigma-\displaystyle\frac{\sigma_x+\sigma_y}{2}=\displaystyle\frac{\sigma_x-\sigma_y}{2} \cos 2\theta+\tau_xy \sen\hspace{0.05cm}2\theta$     (3.50)
$\displaystyle \tau=-\displaystyle\frac{\sigma_x-\sigma_y}{2} \sen\hspace{0.05cm}2\theta+ \tau_{xy} \cos 2\theta$     (3.51)

Si el plano de referencia fuera principal, se verificaría que $ \tau=0$. Así, igualando a cero la ecuación (3.51) se obtiene el ángulo $ \theta$ que forma la dirección principal 1 con el eje $ x$

$\displaystyle \tan 2\theta=\displaystyle\frac{\tau_{xy}}{\displaystyle\frac{\sigma_x-\sigma_y}{2}}$ (3.52)


Subsecciones