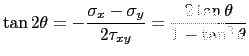 |
(3.59) |
Son las envolventes de las direcciones para las que la tensión tangencial es máxima en cada punto. Forman dos familias de curvas ortogonales que cortan a 45º a las isostáticas.
Las ecuaciones de estas curvas se obtienen a partir de la ecuación
como
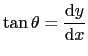 |
Sustituyendo esta expresión en (3.59), se obtiene
que es una ecuación de segundo grado en
![]() , cuyas raíces son
, cuyas raíces son