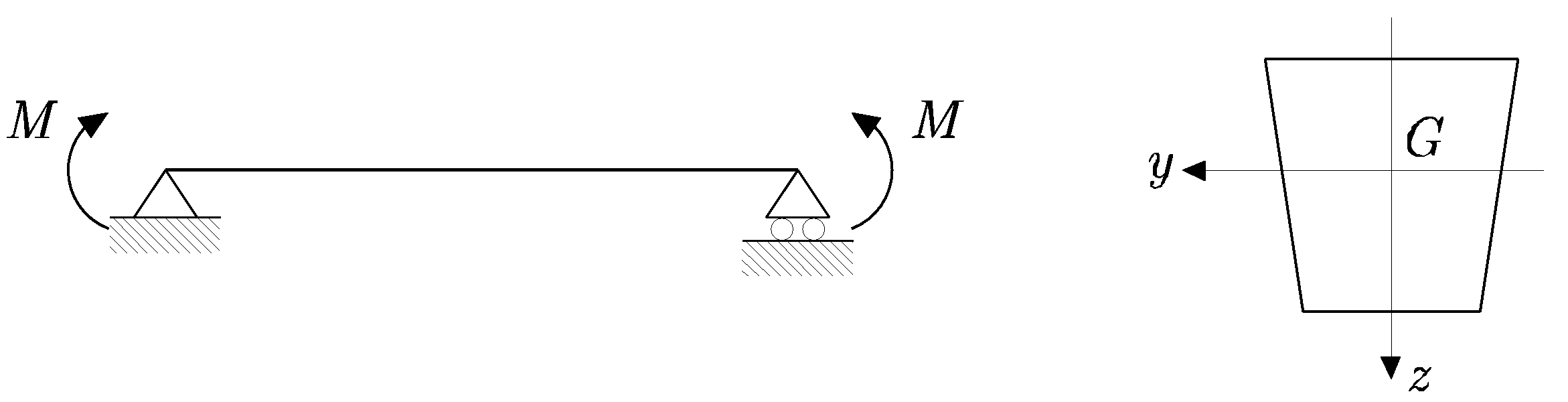 |
Sea una barra prismática con sección transversal simétrica sometida a dos momentos iguales y de signo contrario en sus extremos, considerándose que actúan solamente en el plano de simetría (XZ), tal como se muestra en la Figura 8.3.
Se considerarán dos hipótesis de partida:
Debido a la acción de los momentos flectores la viga flecta en el plano XZ. Las secciones transversales permanecen rectas y planas aunque giran respecto de sí mismas. Las fibras de la cara inferior de la barra se alargan (se traccionan) y las de la cara superior se acortan (se comprimen). La superficie comprendida entre las dos superficies extremas, cuyas fibras ni se alargan ni se acortan, se denomina superficie neutra. La Figura 8.4 a) muestra gráficamente la superficie neutra de una barra sometida a acciones exteriores.
La intersección de dicha superficie con el plano de simetría de la barra se denomina fibra neutra. La intersección de la superficie neutra con cualquier sección transversal se denomina eje neutro. La Figura 8.4 b) muestra gráficamente la fibra neutra y el eje neutro de una barra sometida a acciones exteriores.
Se estudiará una rebanada nmpq de la barra, de longitud dx. La fibra neutra se representa por la línea AB que se muestra en la Figura 8.5 a). Las secciones transversales nm y pq permanecen rectas y planas, tal como se muestra en la Figura 8.5 b).
Las trazas de los planos que contienen las secciones transversales mn y pq en la barra deformada forman un ángulo
d![]() y se cortan en el punto O, que es el centro de curvatura de las fibras de la rebanada. El radio de curvatura
y se cortan en el punto O, que es el centro de curvatura de las fibras de la rebanada. El radio de curvatura ![]() (referido a la fibra neutra) permanece constante durante la deformación. Además, la distancia dx entre las dos secciones mn y pq permanece invariable en la superficie neutra, verificándose
(referido a la fibra neutra) permanece constante durante la deformación. Además, la distancia dx entre las dos secciones mn y pq permanece invariable en la superficie neutra, verificándose
El resto de las fibras longitudinales comprendidas entre los dos planos tendrán deformaciones lineales al alargarse o acortarse.
La fibra ef, antes de la deformación, tiene una longitud dx. Tras la deformación, que se muestra en la Figura 8.5 b), su longitud es
y su deformación longitudinal unitaria
De acuerdo con la ley de Hooke, dicha deformación se puede expresar en función de la tensión sobre la fibra y del módulo de elasticidad longitudinal como:
Igualando las expresiones (8.8) y (8.9) se obtiene la denominada Ley de Navier:
En una sección sometida a flexión pura, los módulos de las tensiones actuantes sobre las distintas fibras son directamente proporcionales a sus distancias al eje neutro.
Teniendo en cuenta (8.4) y (8.5), la ley de Navier puede expresarse como
dependiendo de si el momento actúa según el eje y o el z.