 |
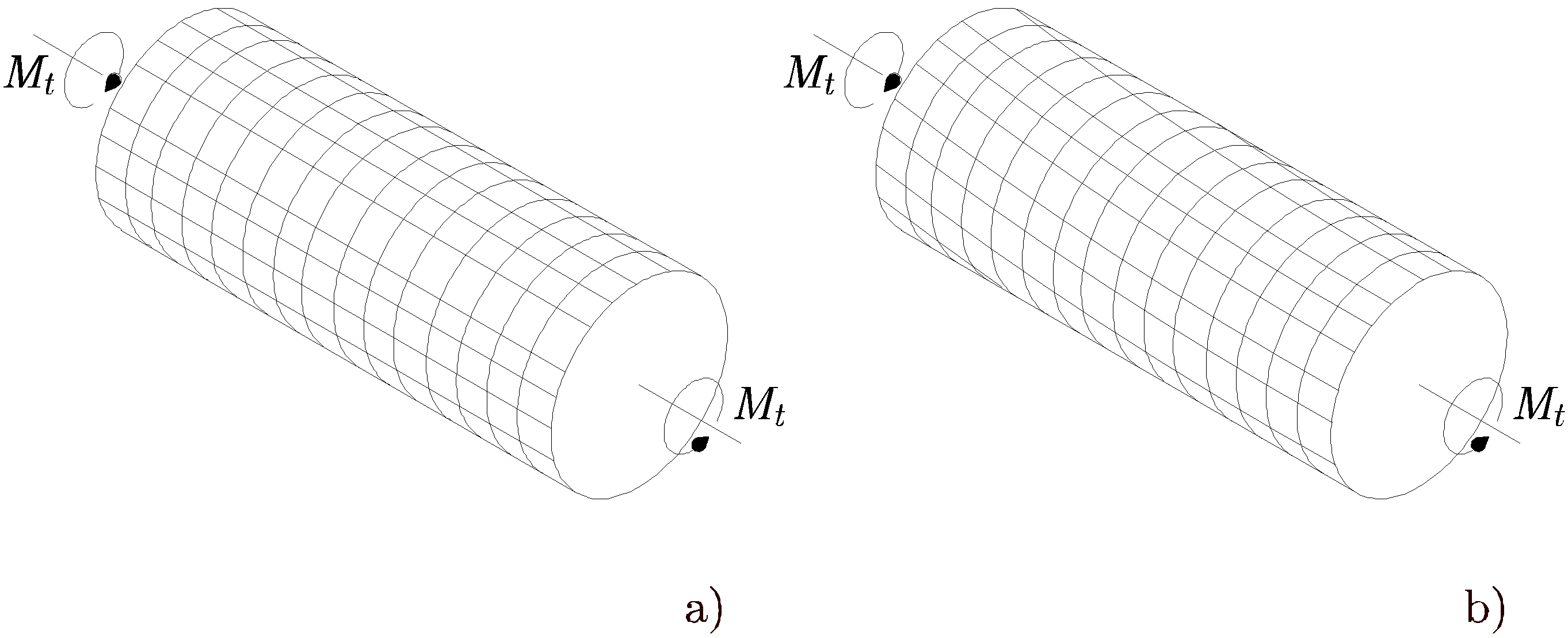
Las barras prismáticas de sección circular son el elemento estructural más común sometido a torsión. Se puede demostrar que debido a la simetría de la sección transversal, las secciones transversales planas normales al eje de la barra permanecen planas durante la deformación y no sufren distorsión en su propio plano. Esto se aprecia en la Figura 11.1. Se ha trazado una rejilla sobre la barra sin deformar, como se muestra en la Figura 11.1 a). Al deformarse, las secciones transversales circulares permanecen siendo circulares y las líneas longitudinales forman hélices que intersecan a los círculos según ángulos iguales.
Sea una rebanada diferencial de la barra, de longitud dx, como se muestra en la Figura 11.2. Se considerará un elemento en la superficie de ésta, definido por sus vértices a, b, c y d. Los lados ab y cd son inicialmente paralelos al eje longitudinal. Durante la torsión de la barra, las secciones transversales extremas giran una respecto a la otra un ángulo
d![]() , de manera que, considerando como referencia la sección extrema de la izquierda, los puntos b y c pasan a la posición b' y c'. Se considera que las longitudes de los lados del elemento, ahora ab' y dc', no han cambiado. Sin embargo, si se ha producido una deformación angular, de valor
, de manera que, considerando como referencia la sección extrema de la izquierda, los puntos b y c pasan a la posición b' y c'. Se considera que las longitudes de los lados del elemento, ahora ab' y dc', no han cambiado. Sin embargo, si se ha producido una deformación angular, de valor
![]() viene expresada en radianes. La distancia ab es la longitud de la rebanada diferencial, dx.
viene expresada en radianes. La distancia ab es la longitud de la rebanada diferencial, dx.
Por otro lado, si r es el radio de la sección transversal, bb' puede expresarse como
![]() d
d![]() , y la ecuación (11.1) como
, y la ecuación (11.1) como
En la ecuación 11.2
![]() es la razón de cambio del ángulo de torsión con respecto a la distancia x medida a lo largo del eje de la barra. Dicha razón se denota con la letra
es la razón de cambio del ángulo de torsión con respecto a la distancia x medida a lo largo del eje de la barra. Dicha razón se denota con la letra ![]() y se denomina ángulo de torsión por unidad de longitud,
y se denomina ángulo de torsión por unidad de longitud,
Sustituyendo en la ecuación (11.2) la (11.3), aquella toma la forma
Como los radios en las secciones transversales permanecen rectos y sin deformar durante la torsión, el análisis realizado anteriormente es válido para cualquier elemento sobre la superficie de un cilindro interior de radio r. Por tanto, la deformación angular tiene la expresión
La ecuación (11.5) implica que las deformaciones angulares en una barra circular varían linealmente con la distancia radial ![]() desde el centro. Es nula en el centro y máxima en la superficie exterior. Esta variación lineal implica que
desde el centro. Es nula en el centro y máxima en la superficie exterior. Esta variación lineal implica que
![]() es constante.
es constante.
Conocida la deformación, el estado tensional se puede determinar a partir de la relación tensión-deformación para el material de la barra. Si el material es elástico y lineal, la ley de Hooke establece como relación entre la tensión y la deformación tangenciales
Sustituyendo (11.2) en (11.6), la tensión tangencial máxima es
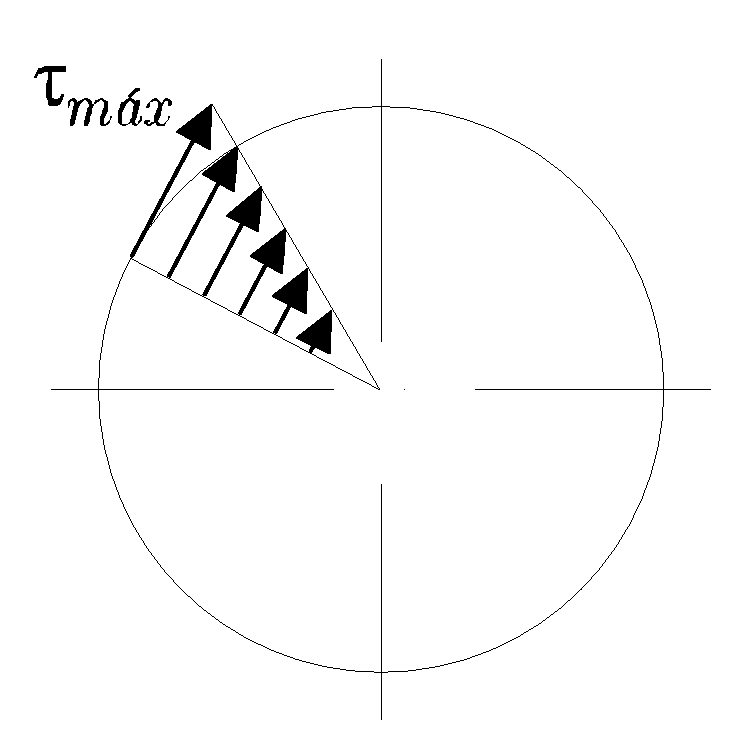
que al igual que las deformaciones, tiene una distribución lineal y es nula en el centro y máximo en la superficie, como se muestra en la Figura 11.3.
 |
El momento torsor resultante de la actuación de la tensión tangencial es
El ángulo de torsión, a partir de la ecuación anterior, es
siendo S el área e ![]() el momento de inercia polar, de la sección transversal.
el momento de inercia polar, de la sección transversal.
Por equilibrio,
![]() es igual en magnitud al momento torsor
es igual en magnitud al momento torsor ![]() aplicado en el extremo de la sección. Expresando las ecuaciones (11.7), (11.8) y (11.9) en función de la solicitación actuante
aplicado en el extremo de la sección. Expresando las ecuaciones (11.7), (11.8) y (11.9) en función de la solicitación actuante
![]() , las constantes del material y la geometría de la barra, e integrando (11.9) a lo largo de la barra, se obtienen las ecuaciones fundamentales de la teoría elemental de la torsión
, las constantes del material y la geometría de la barra, e integrando (11.9) a lo largo de la barra, se obtienen las ecuaciones fundamentales de la teoría elemental de la torsión