Si la distribución de tensiones tangenciales sobre una sección es estáticamente equivalente al esfuerzo cortante, debe verificarse la igualdad de resultante y de momentos respecto a cualquier punto del sistema formado por el esfuerzo cortante y la resultante de la distribución de tensiones tangenciales. La igualdad de la resultante se verifica siempre que la distribución de tensiones tangenciales se haya calculado correctamente. Sin embargo, en el desarrollo realizado para el cálculo de éstas no se ha tenido en cuenta el punto de actuación de la carga (cortante).
Figura 9.10:
Concepto de centro de esfuerzos cortantes
|
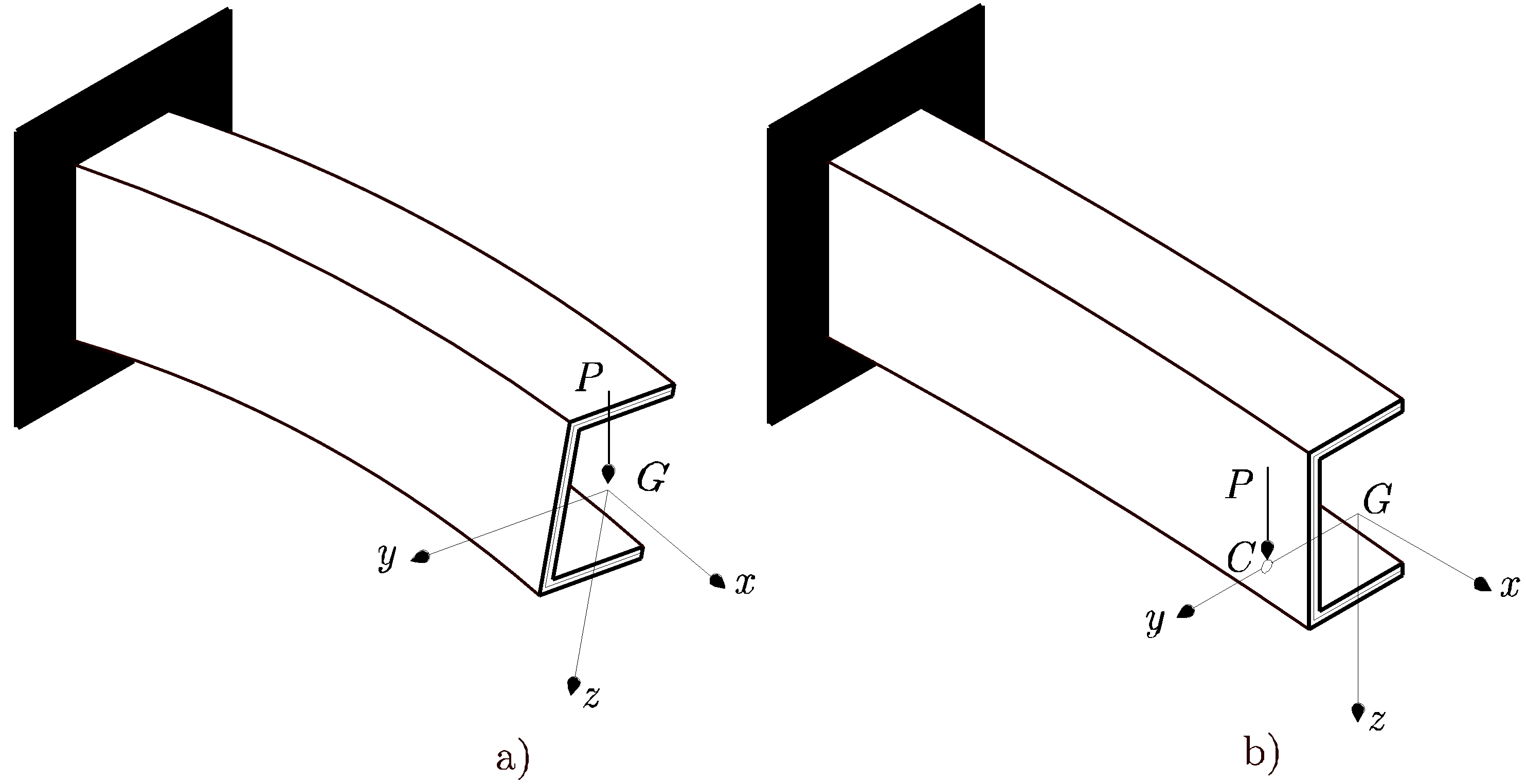 |
En la Figura 9.10 a) se ha considerado la carga P actuando en el centro de gravedad de la sección. La pieza se torsiona a la vez que flecta. Esta torsión es debida a que no existe equivalencia entre el momento que produce el esfuerzo cortante respecto a cualquier punto de la sección y el momento que produce la distribución de tensiones tangenciales. No obstante, existe un punto de aplicación del esfuerzo cortante que hace que se verifique dicha equivalencia. Este punto se denomina centro de esfuerzos cortantes. En la Figura 9.10 b) se muestra como al situar la carga P en el centro de esfuerzos cortantes, C, la viga sólo flecta en el plano XZ.
De lo comentado anteriormente se deducen la siguientes consecuencias:
- Para que una barra prismática sometida a la acción de una carga transversal P trabaje a flexión sin torsión, es necesario que dicha carga pase por el centro de esfuerzos cortantes de la sección en la que actúa. En caso contrario, se producirán en la sección además de tensiones tangenciales debidas a la carga P, tensiones tangenciales debidas a la acción del momento torsor
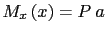 , siendo a la distancia desde el centro de esfuerzos cortantes al punto donde se ha aplicado P, como se muestra en la Figura 9.11.
, siendo a la distancia desde el centro de esfuerzos cortantes al punto donde se ha aplicado P, como se muestra en la Figura 9.11.
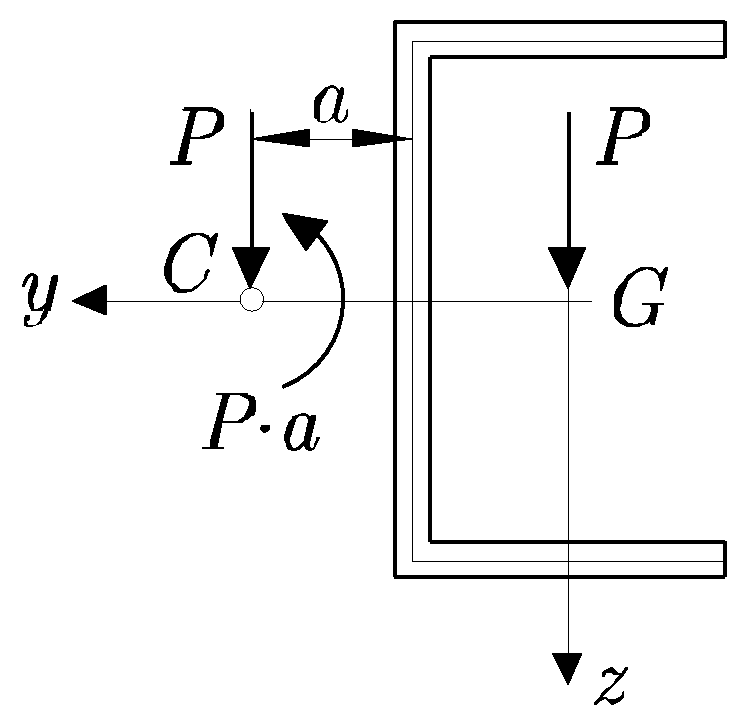
Figura 9.11:
Torsión debida a la no aplicación de la carga en el centro de esfuerzos cortantes
|
 |
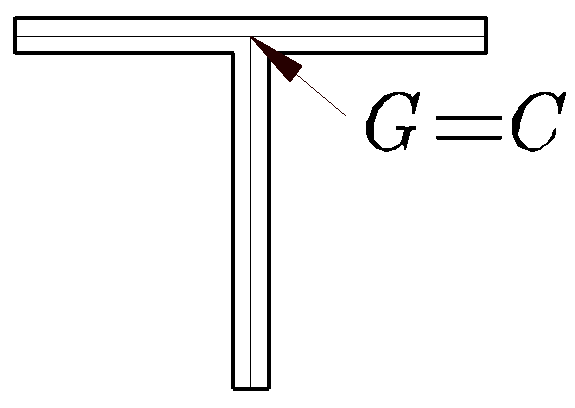
- El centro de esfuerzos cortantes será un punto tal que, el momento de las fuerzas a que dan lugar las tensiones tangenciales respecto de él, sea nulo. Esto es evidente ya que, si sobre ese punto se aplica una carga P, el momento de esta fuerza respecto de dicho punto es nulo y ambos sistemas serían equivalentes. Esta propiedad permite determinar inmediatamente la posición del centro de esfuerzos cortantes en secciones ramificadas que concurran en un punto: como todas las tensiones tangenciales pasan por dicho punto, sus momentos respecto de dicho punto son nulos, y éste será el centro de esfuerzos cortantes, como se muestra en la Figura 9.12.
Figura 9.12:
Centro de esfuerzos cortantes en secciones ramificadas
|
 |
- Si una sección tiene un eje de simetría, sobre él se encontrará el centro de esfuerzos cortantes. Si una sección tiene dos ejes de simetría, la intersección será el centro de esfuerzos cortantes.
