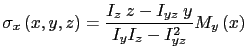 |
(8.2) | ||
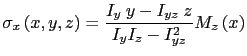 |
(8.3) |
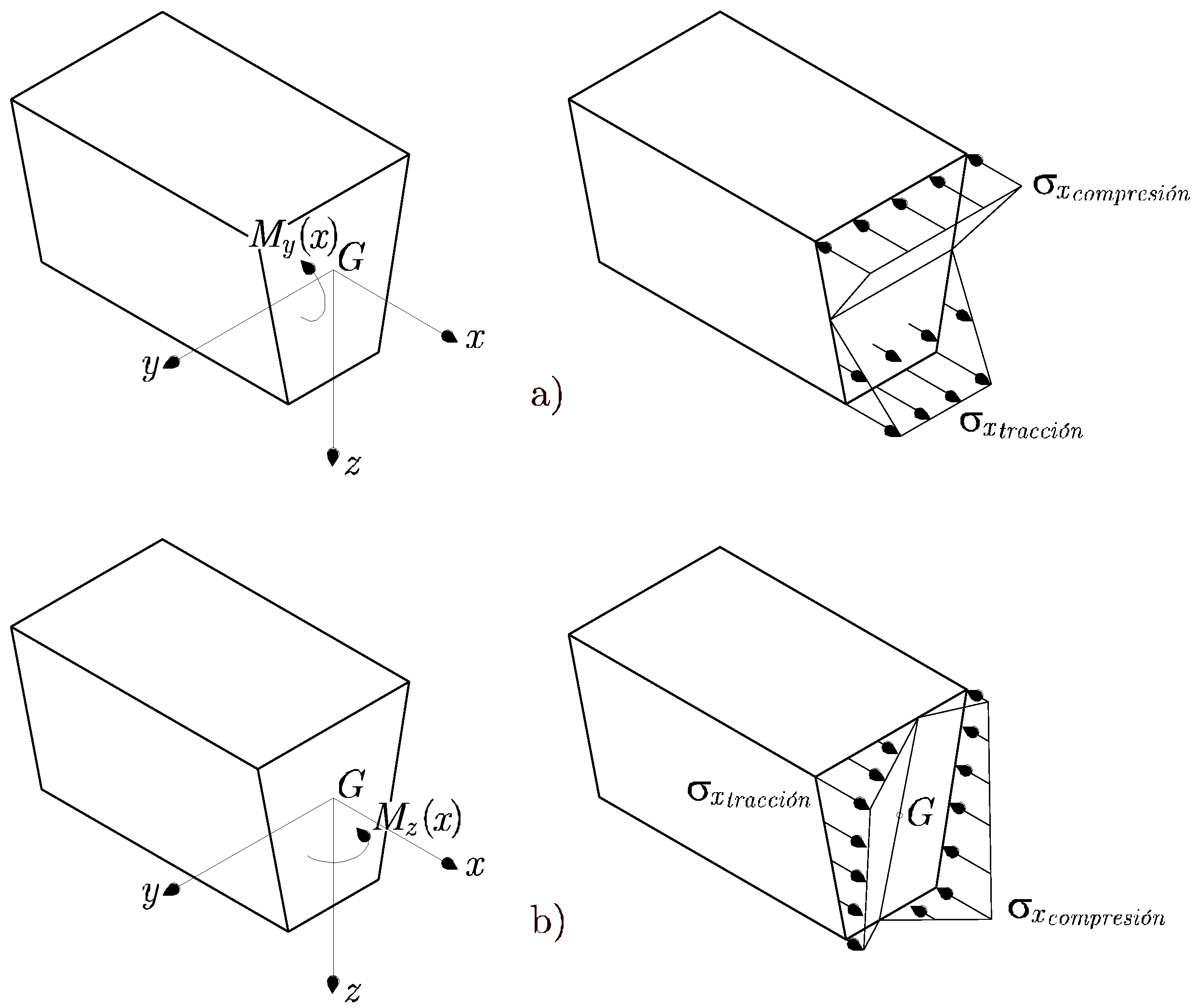
Si el momento flector es uniaxial se dice que la flexión es pura. Las distribuciones de tensiones normales para el momento actuando según el eje y o el eje z son, respectivamente
Si los ejes de referencia son principales de inercia, ![]() , y las expresiones (8.2) y (8.3), se transforman en
, y las expresiones (8.2) y (8.3), se transforman en
En la Figura 8.2 a) y en la Figura 8.2 b) se representan las distribuciones de tensiones normales para los casos de flexión pura según los ejes y y z, respectivamente.
 |