Ecuaciones de equilibrio

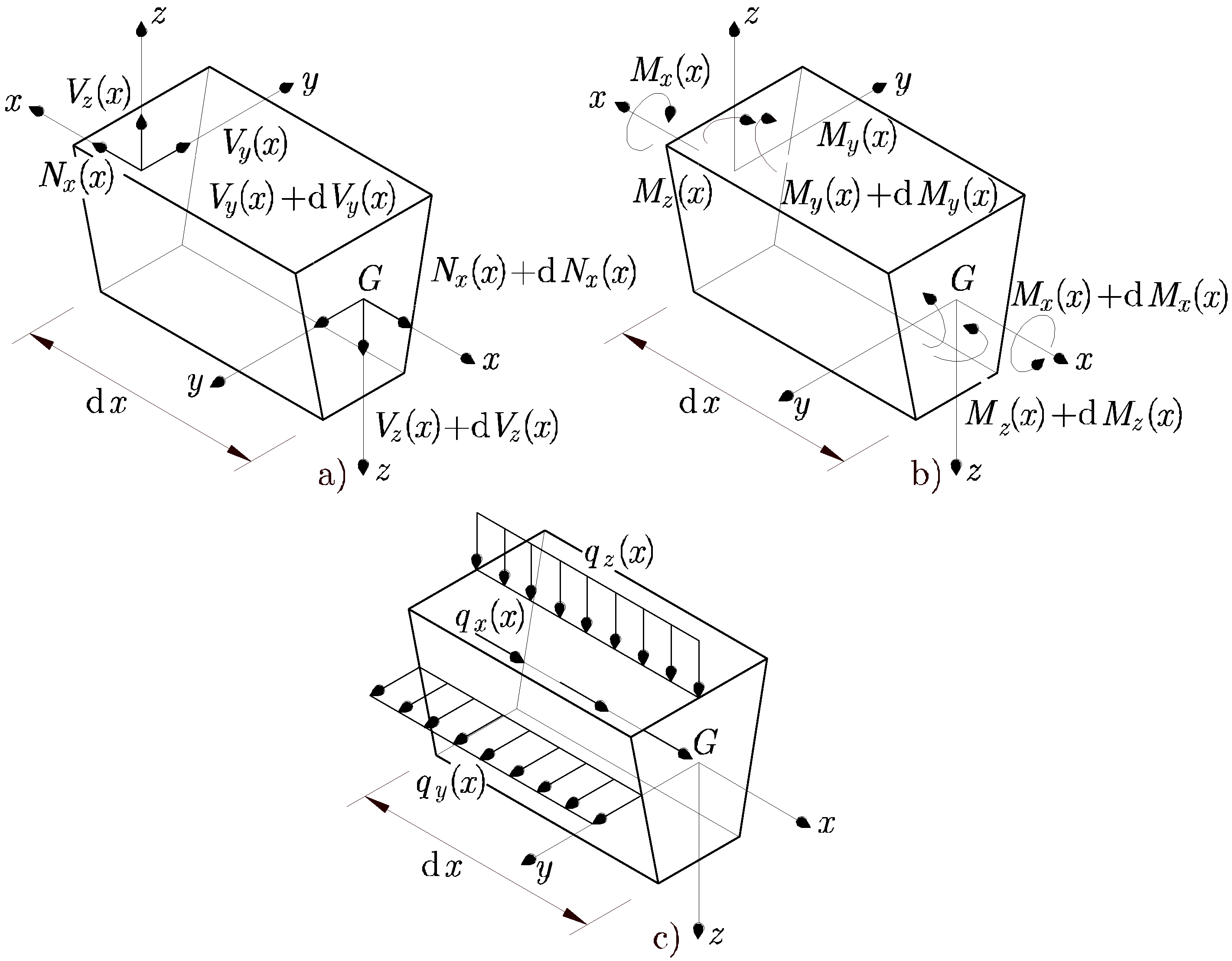
Las ecuaciones de equilibrio interno del modelo de barras se obtienen planteando el equilibrio de fuerzas y momentos que actúan sobre una rebanada diferencial de la barra.

**Figura 6.14:** Esfuerzos y fuerzas actuantes sobre una rebanada

En la Figura 6.14 se muestra una rebanada diferencial de longitud dx y todas las acciones que la solicitan.

En la sección frontal de la rebanada diferencial que se muestra en la Figura 6.14 a) y Figura 6.14 b), actúan los esfuerzos $N_x\left(x\right)$ , $V_y\left(x\right)$ , $V_z\left(x\right)$ , $M_x\left(x\right)$ , $M_y\left(x\right)$ y $M_z\left(x\right)$ , que son estáticamente equivalentes a la distribución del vector tensión en los puntos de dicha sección. En la sección dorsal de la rebanada diferencial actúan esos mismos esfuerzos incrementados una cantidad diferencial, $N_x\left(x\right)+$ d $N_x\left(x\right)$ , $V_y\left(x\right)+$ d $V_y\left(x\right)$ , $V_z\left(x\right)+$ d $V_z\left(x\right)$ , $M_x\left(x\right)+$ d $M_x\left(x\right)$ , $M_y\left(x\right)+$ d $M_y\left(x\right)$ y $M_z\left(x\right)+$ d $M_z\left(x\right)$ . Finalmente, hay aplicadas unas cargas $q_x\left(x\right)$ , $q_y\left(x\right)$ y $q_z\left(x\right)$ y unos momentos $g_x\left(x\right)$ , $g_y\left(x\right)$ y $g_z\left(x\right)$ , que se muestran en la Figura 6.14 c), repartidos uniformemente sobre la longitud dx (los momentos distribuidos uniformemente no se han representado).

Imponiendo el equilibrio de fuerzas y momentos en la rebanada diferencial, al igual que se hace en Elasticidad con las tensiones a nivel de punto, se obtienen las seis ecuaciones de equilibrio interno.

El equilibrio de fuerzas en la dirección x es

$\displaystyle N_x\left(x\right)+$ d $\displaystyle N_x\left(x\right)-N_x\left(x\right)+q_x\left(x\right)$ d $\displaystyle x=0$

(6.9)

obteniéndose que

$\displaystyle \displaystyle\frac{\text{d}N_x\left(x\right)}{\text{d}x}+q_x\left(x\right)=0$

(6.10)

Los equilibrios de fuerzas en las direcciones y y z son

	$\displaystyle V_y\left(x\right)+$ d $\displaystyle V_y\left(x\right)-V_y\left(x\right)+q_y\left(x\right)$ d $\displaystyle x=0$	(6.11)
	$\displaystyle V_z\left(x\right)+$ d $\displaystyle V_z\left(x\right)-V_z\left(x\right)+q_z\left(x\right)$ d $\displaystyle x=0$	(6.12)

obteniéndose que

	$\displaystyle \displaystyle\frac{\text{d}V_y\left(x\right)}{\text{d}x}+q_y\left(x\right)=0$	(6.13)
	$\displaystyle \displaystyle\frac{\text{d}V_z\left(x\right)}{\text{d}x}+q_z\left(x\right)=0$	(6.14)

Por último, se establecerán los equilibrios de momentos. El equilibrio de momentos alrededor del eje x es

$\displaystyle M_x\left(x\right)+$ d $\displaystyle M_x\left(x\right)-M_x\left(x\right)+g_x\left(x\right)$ d $\displaystyle x=0$

(6.15)

despejando se obtiene

$\displaystyle \displaystyle\frac{\text{d}M_x\left(x\right)}{\text{d}x}+g_x\left(x\right)=0$

(6.16)

Los equilibrios de momentos alrededor de los ejes y y z son

	$\displaystyle M_y\left(x\right)+$ d $\displaystyle M_y\left(x\right)-M_y\left(x\right)-V_z\left(x\right)$ d $\displaystyle x+g_y\left(x\right)$ d $\displaystyle x+q_z\left(x\right)$ d $\displaystyle x\displaystyle\frac{\text{d}x}{2}=0$	(6.17)
	$\displaystyle M_z\left(x\right)+$ d $\displaystyle M_z\left(x\right)-M_z\left(x\right)-V_y\left(x\right)$ d $\displaystyle x+g_z\left(x\right)$ d $\displaystyle x+q_y\left(x\right)$ d $\displaystyle x\displaystyle\frac{\text{d}x}{2}=0$	(6.18)

Despreciando el infinitésimo de orden superior $\left(\text{d}x^2\right)$ , se obtiene

	$\displaystyle \displaystyle\frac{\text{d}M_y\left(x\right)}{\text{d}x}-V_z\left(x\right)+g_y\left(x\right)=0$	(6.19)
	$\displaystyle \displaystyle\frac{\text{d}M_z\left(x\right)}{\text{d}x}-V_y\left(x\right)+g_z\left(x\right)=0$	(6.20)

Si se considera que la sección es simétrica respecto al plano XZ, y que todas las cargas actúan sobre dicho plano, se puede pasar al modelo plano de rebanada que se muestra en la Figura 6.15.

**Figura 6.15:** Equilibrio de una rebanada considerando todas las cargas actuando en el plano XZ

Estableciendo el equilibrio entre fuerzas y esfuerzos, las ecuaciones de equilibrio interno son:

$\displaystyle \displaystyle\frac{\text{d}N_x\left(x\right)}{\text{d}x}+q_x\left(x\right)$	$\displaystyle =$	(6.21)
$\displaystyle \displaystyle\frac{\text{d}V_z\left(x\right)}{\text{d}x}+q_z\left(x\right)$	$\displaystyle =$	(6.22)
$\displaystyle \displaystyle\frac{\text{d}M_y\left(x\right)}{\text{d}x}-V_z\left(x\right)$	$\displaystyle =$	(6.23)

De las ecuaciones (6.21), (6.22) y 6.23, se deduce:

De la expresión (6.21) se deduce que en cualquier tramo de una viga con , el esfuerzo axil $N_x\left(x\right)$ es constante.
De las ecuaciones (6.22) y (6.23) se deduce que en cualquier tramo de una viga con , el esfuerzo cortante $V_z\left(x\right)$ es constante y $M_y\left(x\right)$ varía linealmente.
En tramos de una viga con $q_z \neq 0$ , el esfuerzo cortante $V_z\left(x\right)$ y el momento flector $M_y\left(x\right)$ varían con leyes continuas de primer y segundo grado, respectivamente, si es constante. Estas leyes serían de segundo y tercer grado, respectivamente, si variara linealmente.
De la ecuación (6.23) se deduce que si en un tramo $V_z\left(x\right)=0$ , $M_y\left(x\right)$ es constante. Si $V_z\left(x\right)$ es distinto de cero, $M_y\left(x\right)$ existe y es variable.
De la expresión (6.23) se deduce que para las secciones en que el esfuerzo cortante se anula, el momento flector se hace máximo. No puede ser mínimo porque la derivada segunda de $M_y\left(x\right)$ es negativa, ya que

$\displaystyle q_z\left(x\right)=-\displaystyle\frac{\text{d}V_z\left(x\right)}{\text{d}x}$ (6.24)

que sustituida en (6.23)

$\displaystyle q_z\left(x\right)=-\displaystyle\frac{\text{d}V_z\left(x\right)}{... ...ight)}{\text{d}x}=-\displaystyle\frac{\text{d}^2M_y\left(x\right)}{\text{d}x^2}$ (6.25)