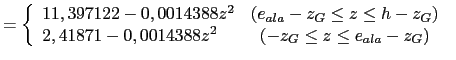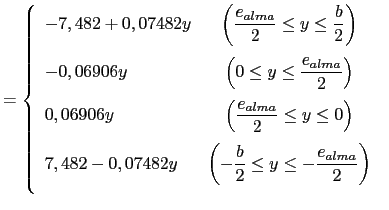Ejercicio 1
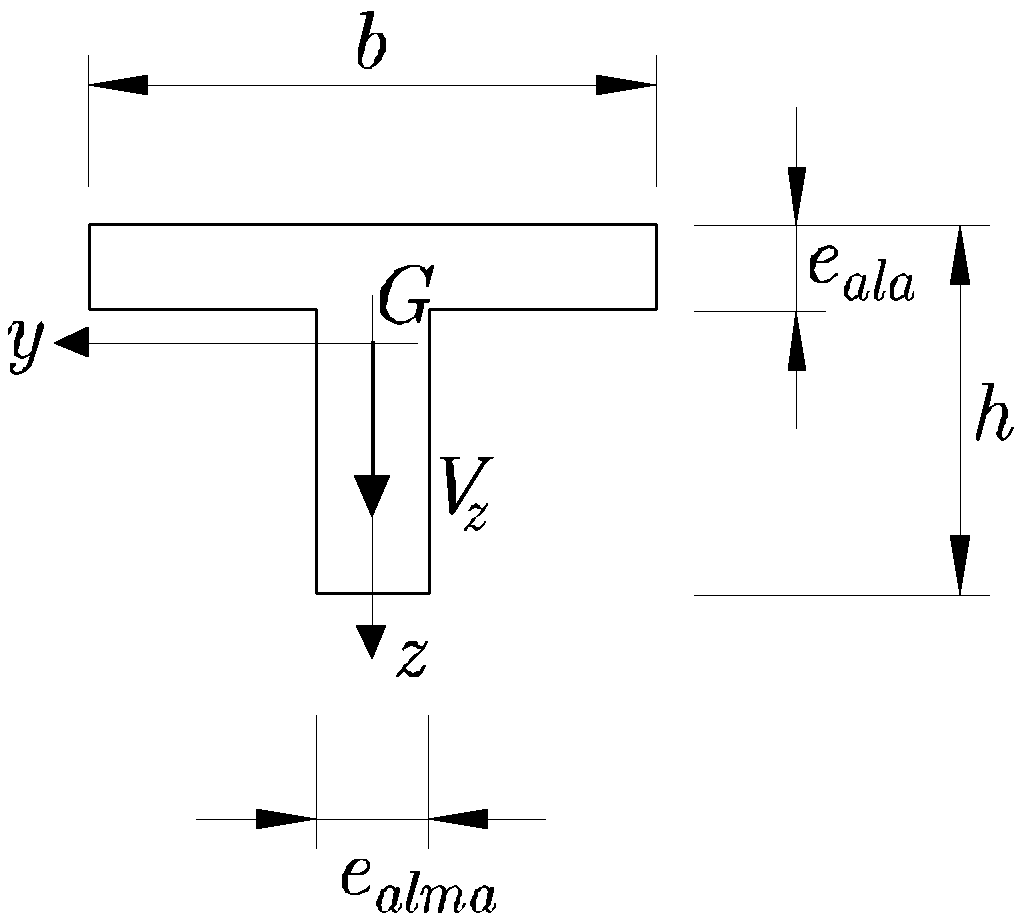
La sección transversal de una viga en T está sometida a un esfuerzo cortante 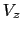 , según se muestra en la Figura 9.13.
, según se muestra en la Figura 9.13.
Figura 9.13:
Sección llena en T sometida a esfuerzo cortante
|
 |
Obtener:
- Las propiedades estáticas de la sección: área
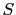 e inercias principales
e inercias principales 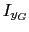 ,
, 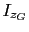
- La expresión analítica de la distribución de tensiones tangenciales
- La representación gráfica de la distribución de tensiones tangenciales
Datos:
Solución:
- Las propiedades estáticas de la sección: área
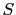 e inercias principales
e inercias principales 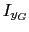 ,
, 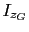
- La expresión analítica de la distribución de tensiones tangenciales
Utilizando como unidades de fuerza N y de longitud mm
- La representación gráfica de la distribución de tensiones tangenciales
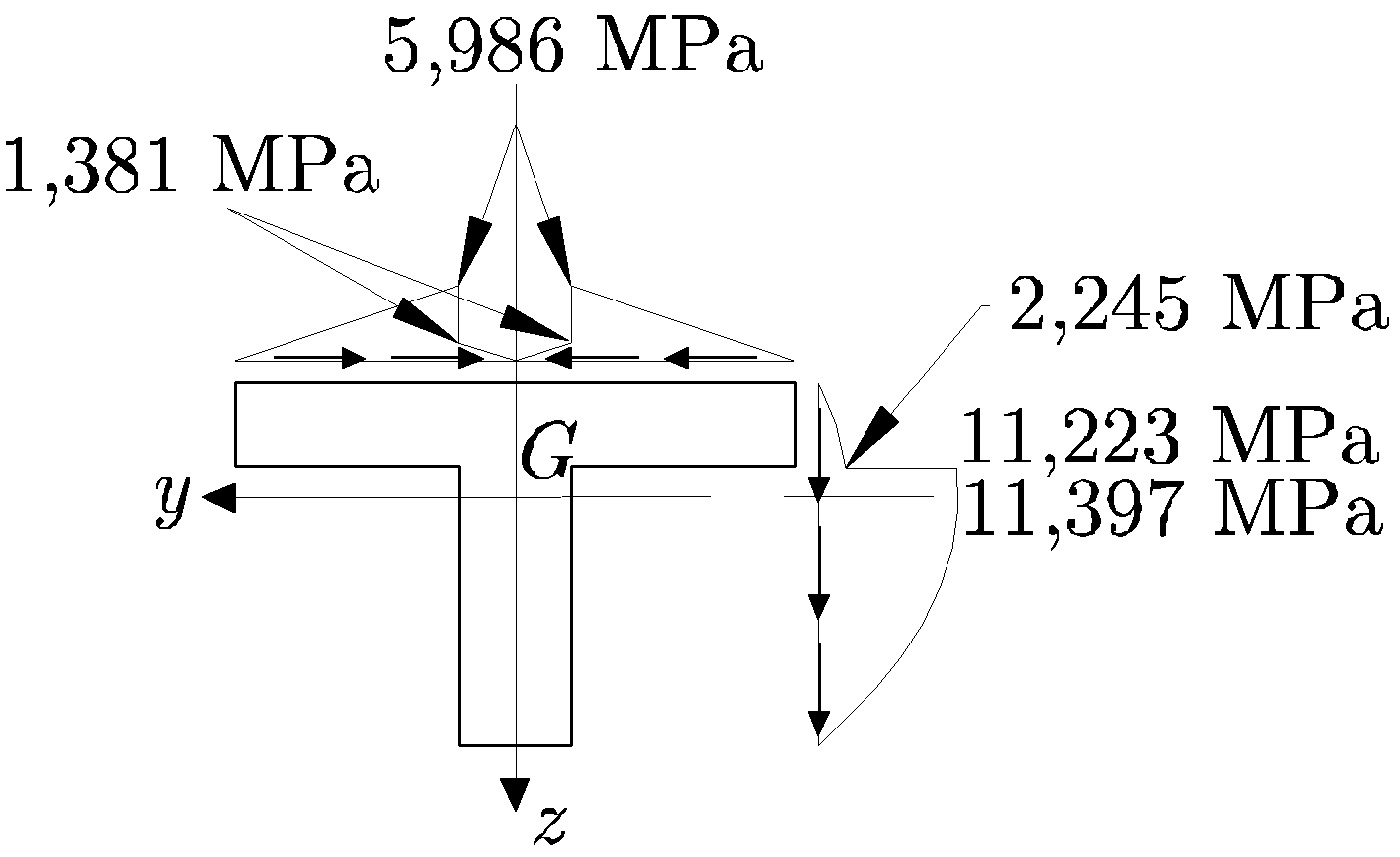
Figura 9.14:
Sección llena en T sometida a esfuerzo cortante. Distribución de tensiones tangenciales
|
 |
Ejercicio 2
La sección transversal que se muestra en la Figura 9.15 está sometida a un esfuerzo cortante 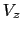 .
.
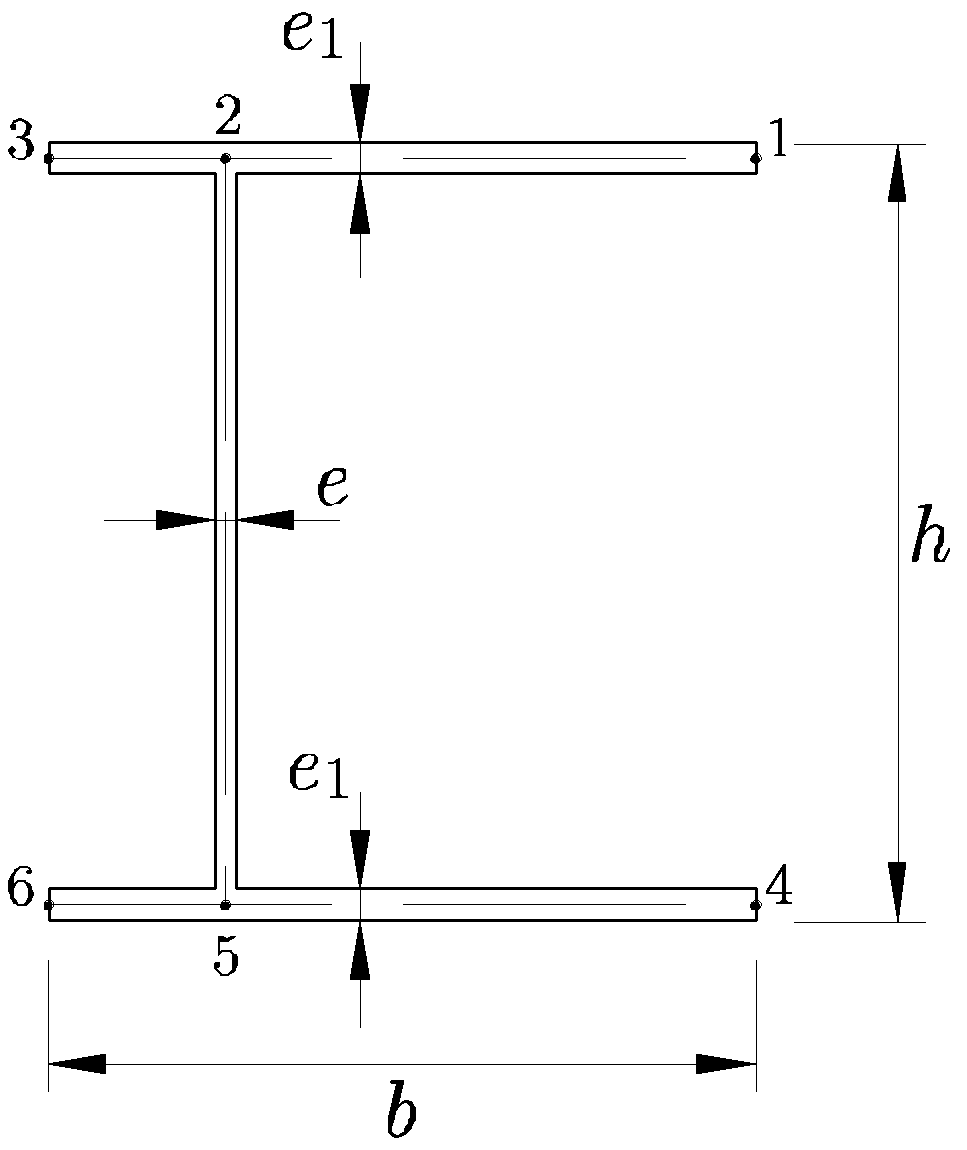
Figura 9.15:
Sección de pared delgada en doble T asimétrica sometida a esfuerzo cortante
|
 |
Obtener:
- Las propiedades estáticas de la sección: área
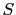 e inercias principales
e inercias principales 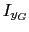 ,
, 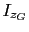
- La expresión analítica de la distribución de tensiones tangenciales
- La representación gráfica de la distribución de tensiones tangenciales
Datos:
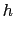 |
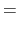 |
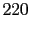 mm , mm ,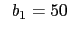 mm , mm ,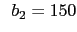 mm , mm ,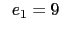 mm , mm ,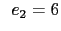 mm mm |
|
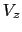 |
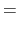 |
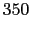 kN kN |
|
Solución:
- Las propiedades estáticas de la sección: área
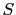 e inercias principales
e inercias principales 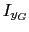 ,
, 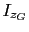
- La expresión analítica de la distribución de tensiones tangenciales
- La representación gráfica de la distribución de tensiones tangenciales
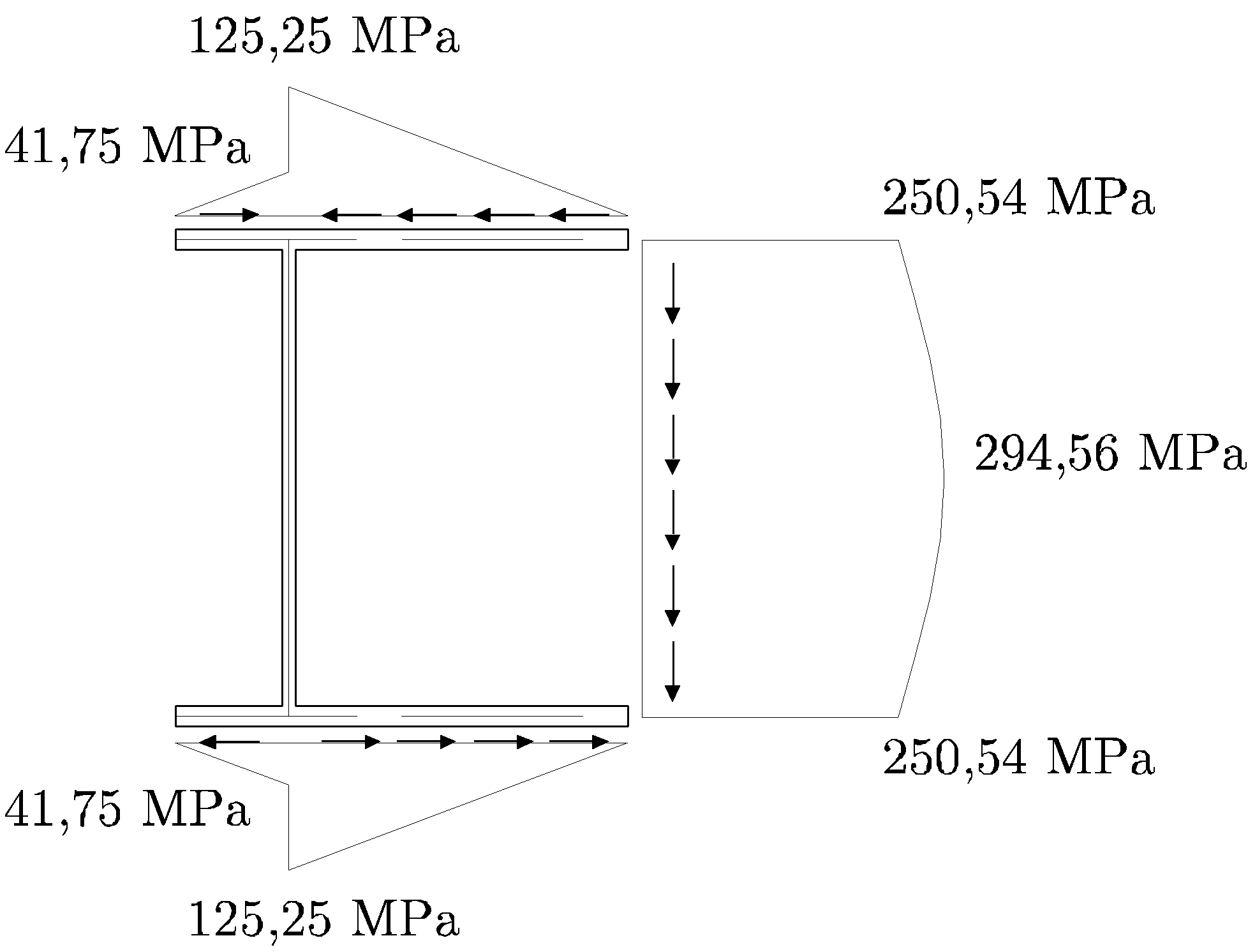
Figura 9.16:
Sección de pared delgada en doble T asimétrica sometida a esfuerzo cortante. Distribución de tensiones tangenciales debidas a un cortante según z
|
 |
Ejercicio 3
Para la sección que se muestra en la Figura 9.15, determinar:
- El centro de esfuerzos cortantes
Solución:
- Obtener el centro de esfuerzos cortantes
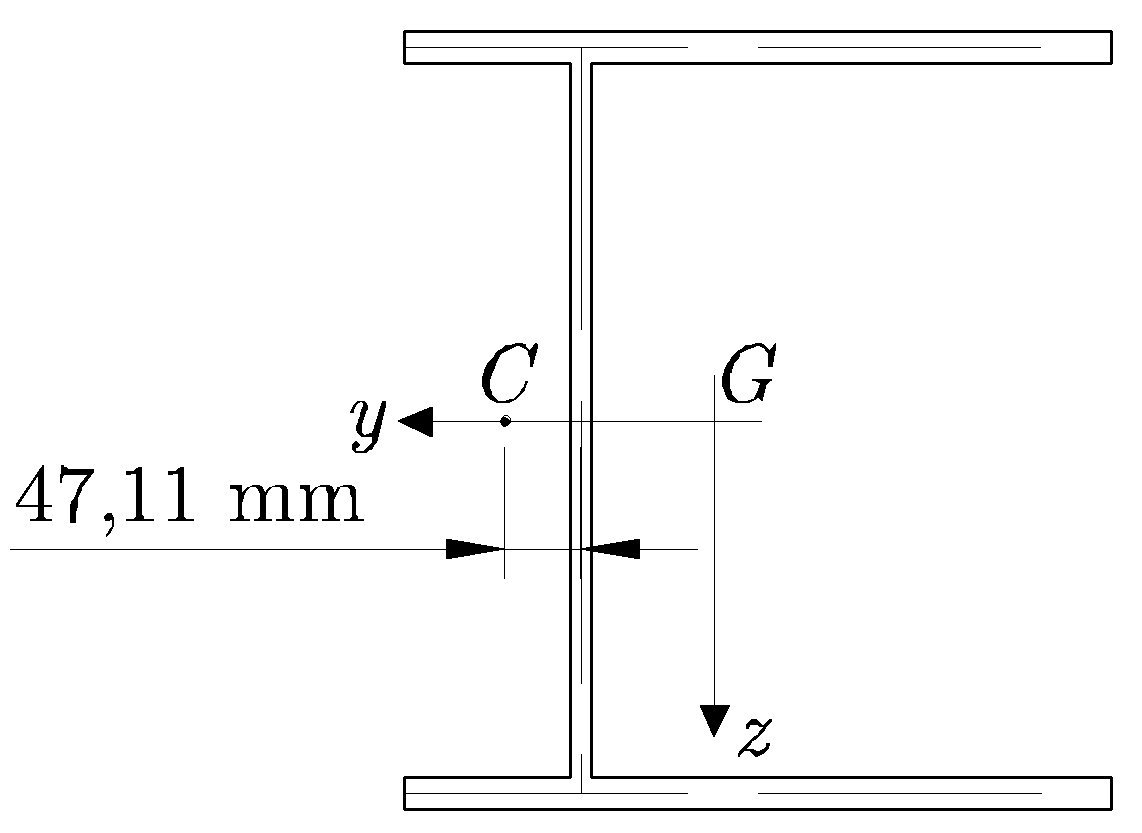
Figura 9.17:
Sección de pared delgada en doble T asimétrica sometida a esfuerzo cortante. Centro de esfuerzos cortantes
|
 |
![]() , según se muestra en la Figura 9.13.
, según se muestra en la Figura 9.13.