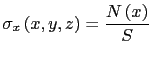Distribución de tensiones normales estáticamente equivalentes a esfuerzos axiles

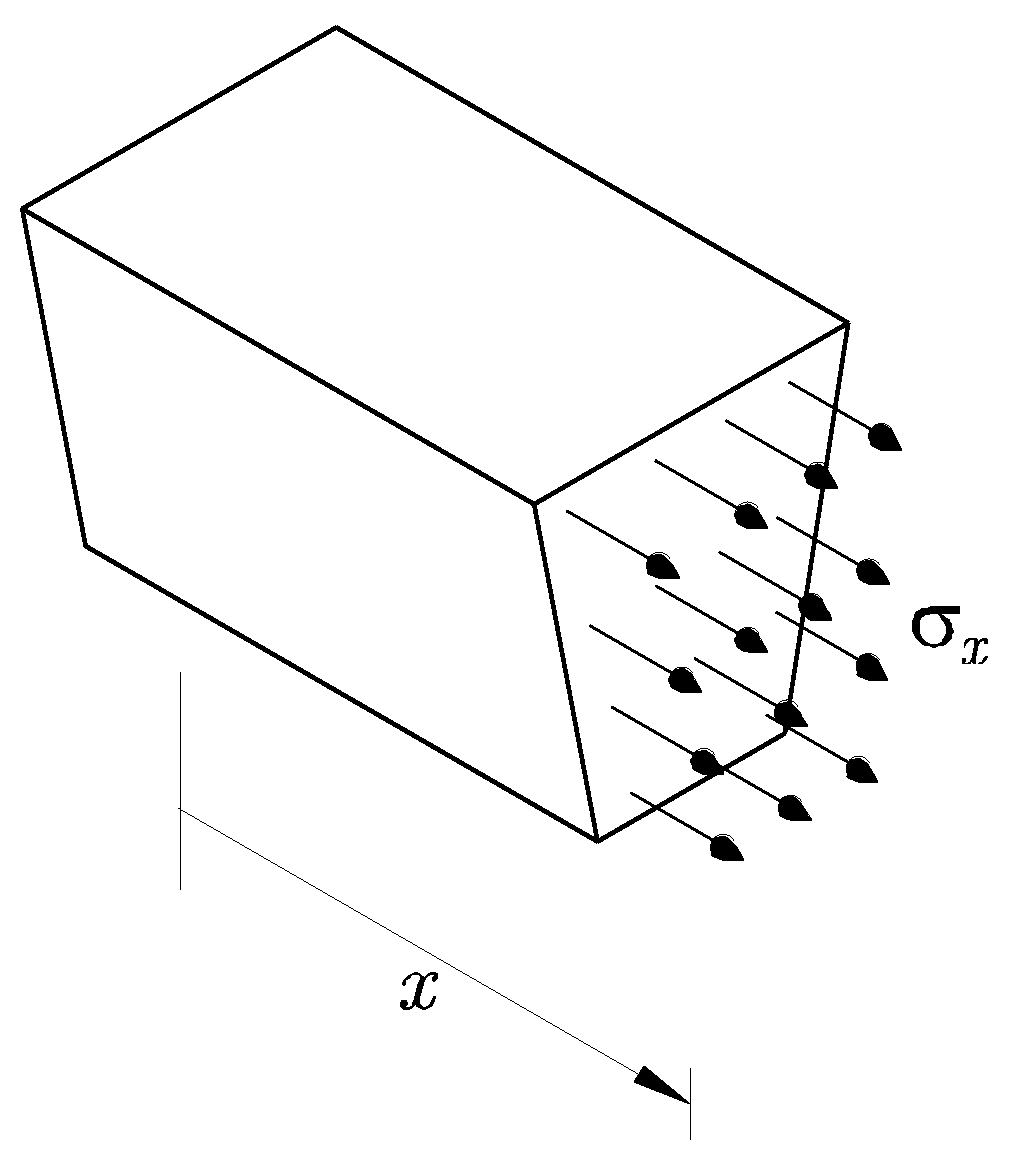
Una barra prismática trabaja a esfuerzo axil, de tracción o compresión, cuando al deformarse desarrolla en cada sección normal a la directriz de la barra (sección recta), tensiones estáticamente equivalentes a un esfuerzo axil. Esto implica que los esfuerzos cortantes y los momentos flectores y torsor son nulos.0 Por tanto, la distribución de tensiones normales viene dada por la expresión La distribución de tensiones normales es

(7.1)

En este tipo de solicitación, el eje neutro nunca corta a la sección. Se ha comprobado experimentalmente que en una barra sometida exclusivamente a esfuerzo axil, cualquier sección transversal recta y plana, sigue siendo recta y plana tras la deformación. Es decir, todos los puntos de una sección tienen la misma deformación. Si la sección es homogénea, la distribución de tensiones es uniforme en toda la sección. El tensor de tensiones en cualquier punto de la sección, es

(7.2)

En la Figura 7.1 se representa la distribución de tensiones correspondiente.

Figura 7.1: Distribución uniforme de tensiones en una sección sometida exclusivamente a esfuerzo axil

En una barra con sección transversal constante sometida a un esfuerzo axil constante, todos y cada uno de los puntos de cualquier sección transversal de la barra, y todas y cada una de las secciones (por tanto todos los puntos de la barra) tendrán la misma tensión. Si la sección y/o el esfuerzo axil no son constantes, la distribución de tensiones será uniforme en cada sección, pero variará su valor de una sección a otra. Un ejemplo sería un cable colgado que resiste la acción de su propio peso.

Figura 7.2: Esfuerzos y tensiones en una sección inclinada respecto a la directriz, de una barra sometida a exclusivamente a esfuerzo axil

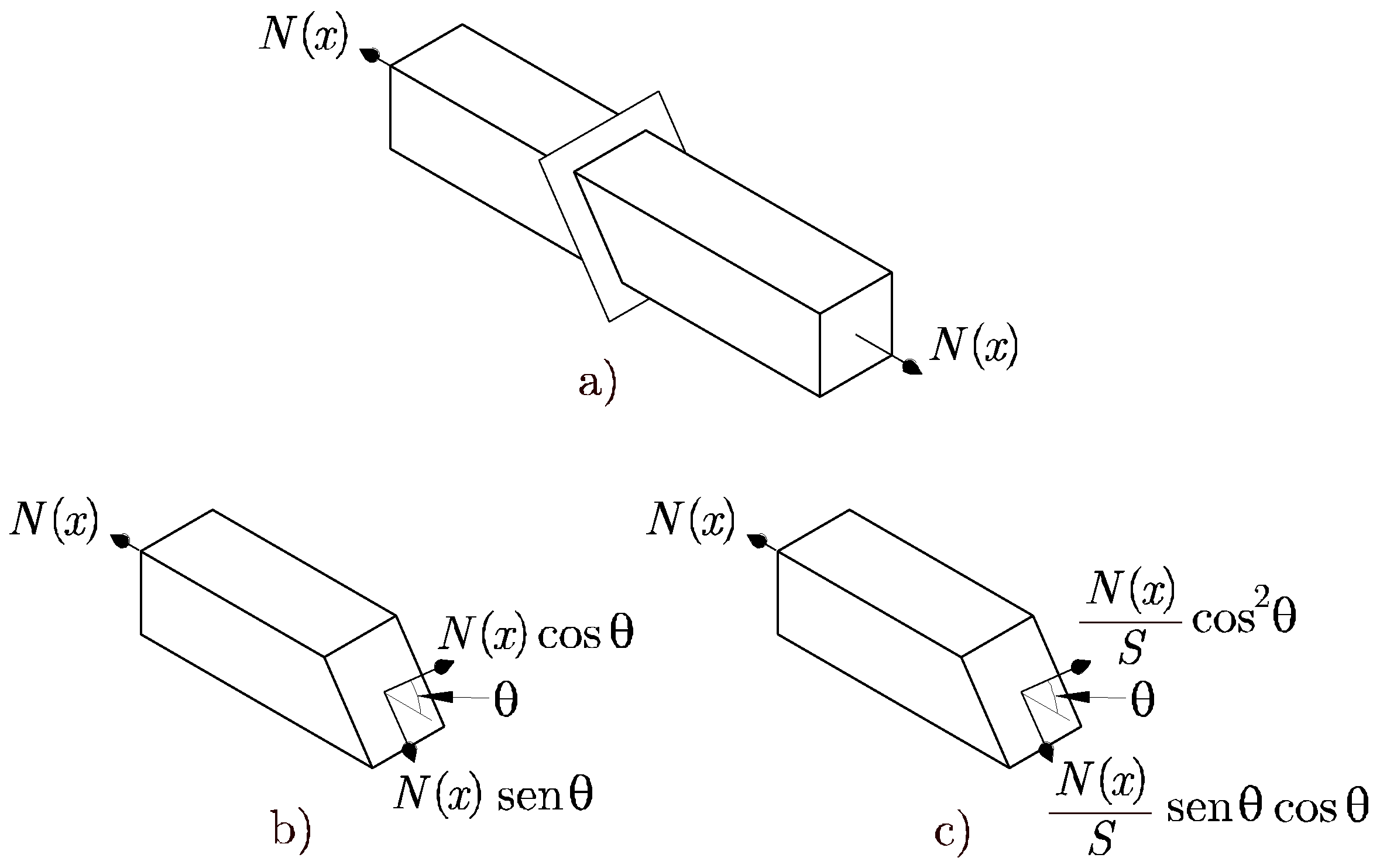El estado tensional en cualquier punto de una sección que no sea recta, como la que se muestra en la Figura 7.2 a), se obtiene descomponiendo la fuerza axil actuante en una componente normal y otra tangencial al plano considerado, como se muestra en la Figura 7.2 b). Las tensiones correspondientes se obtienen al dividir dichas componentes por el área S de la sección inclinada, tal y como se muestra en la Figura 7.2 c).

En la Figura 7.3 se muestra el círculo de Mohr que representa un estado tensional de tracción uniaxial. Se comprueba que dependiendo del plano considerado, pueden existir tensiones tangenciales. La máxima tensión tangencial ( en la figura) corresponde al plano que forma con la directriz de la pieza.

Figura 7.3: Círculo de Mohr para un estado de tracción uniaxial