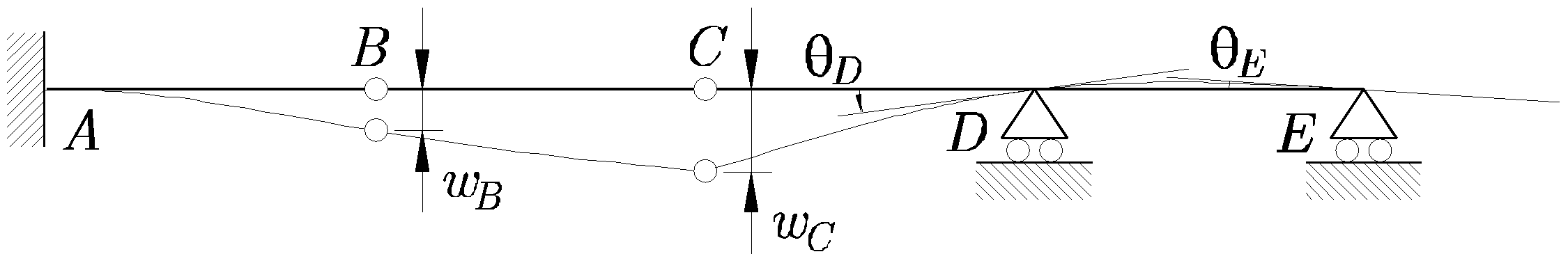Ejercicios propuestos - Tema 13: Desplazamientos en flexión

Ejercicio 1

Para la viga de la Figura 13.7

Figura 13.7: Viga articulada-empotrada con rótula intermedia y cargas distribuidas uniformemente
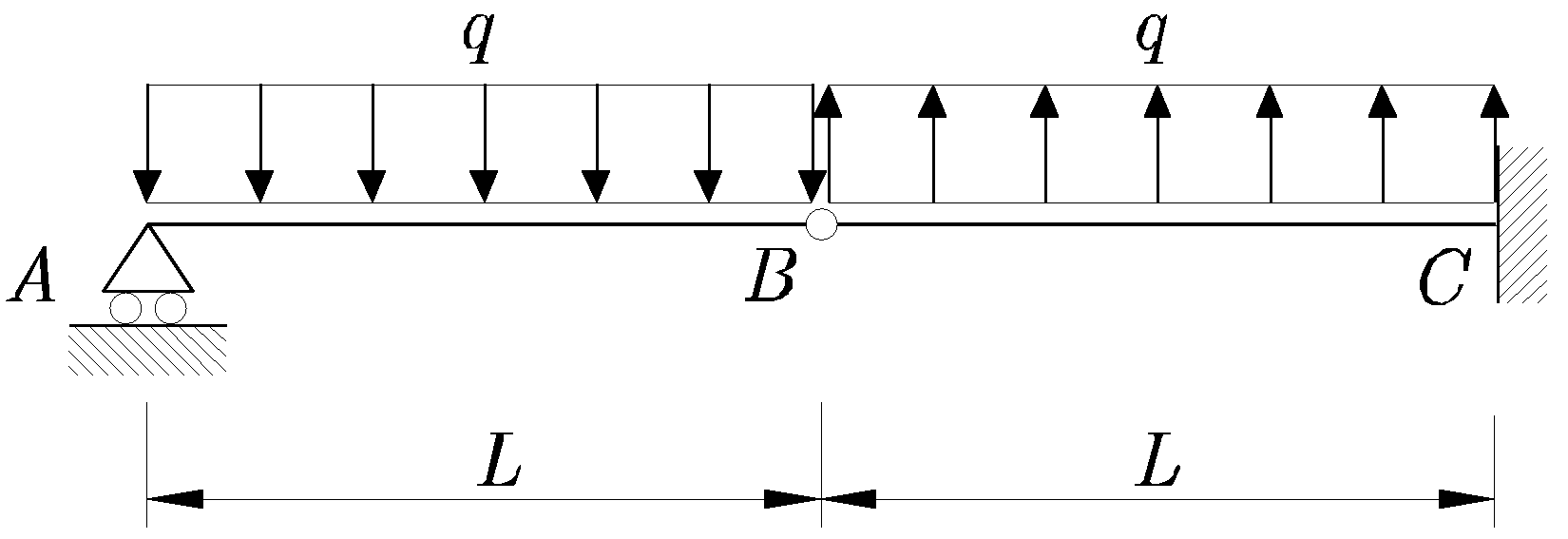Image 1-DFlexion-ejercicio

Obtener, utilizando la ecuación diferencial de segundo orden de la curva elástica:

  1. Las ecuaciones de la curva elástica y de giros
  2. El desplazamiento vertical del punto B
  3. El giro del nudo A
  4. La deforma aproximada de la estructura

Datos:


$\displaystyle L$ $\displaystyle =$ $\displaystyle 4$    m  
$\displaystyle I_y$ $\displaystyle =$ $\displaystyle 5,5\cdot 10^{-4}$    mm$\displaystyle ^4$  
$\displaystyle q$ $\displaystyle =$ $\displaystyle 17$    kN/m  
$\displaystyle E$ $\displaystyle =$ $\displaystyle 20$    GPa  

Solución:

  1. Las ecuaciones de la curva elástica y de giros

    $\displaystyle w'$ $\displaystyle = \left\{ \begin{array}{lc} \dfrac{1}{EI_y}\left[2,833x^3-17x^2... ...,833x^3+51x^2-272x+362,666\right] & 0 \leq x \leq L \\ \end{array} \right.\ $      

    $\displaystyle w$ $\displaystyle = \left\{ \begin{array}{lc} \dfrac{1}{EI_y}\left[0,708x^4-5,666... ...8x^4+17x^3-136x^2+362,666\right] & L \leq x \leq 2L \\ \end{array} \right.\ $      

  2. El desplazamiento vertical del punto B

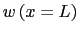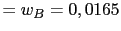    $\displaystyle w\left(x=L\right)$ $\displaystyle = w_B=0,0165$    m      

  3. El giro del nudo A

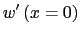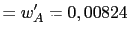    $\displaystyle w'\left(x=0\right)$ $\displaystyle = w'_A=0,00824$    radianes      

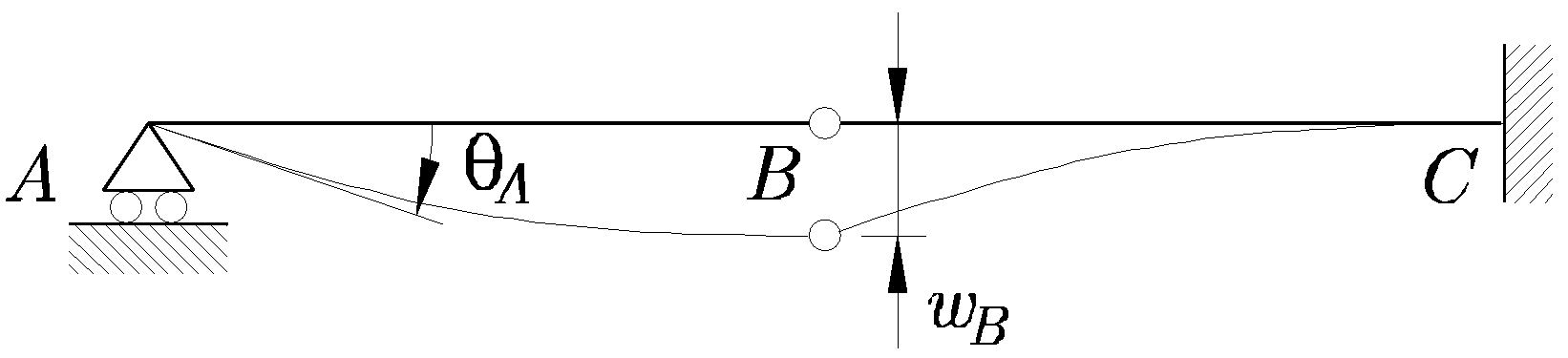
  4. La deforma aproximada de la estructura

    Figura 13.8: Viga articulada-empotrada con rótula intermedia y cargas distribuidas uniformemente. Deformada aproximada
    Image 2-DFlexion-ejercicio

Ejercicio 2

Para la viga de la Figura 13.9

Figura 13.9: Viga biapoyada con cargas triangulares simétricas
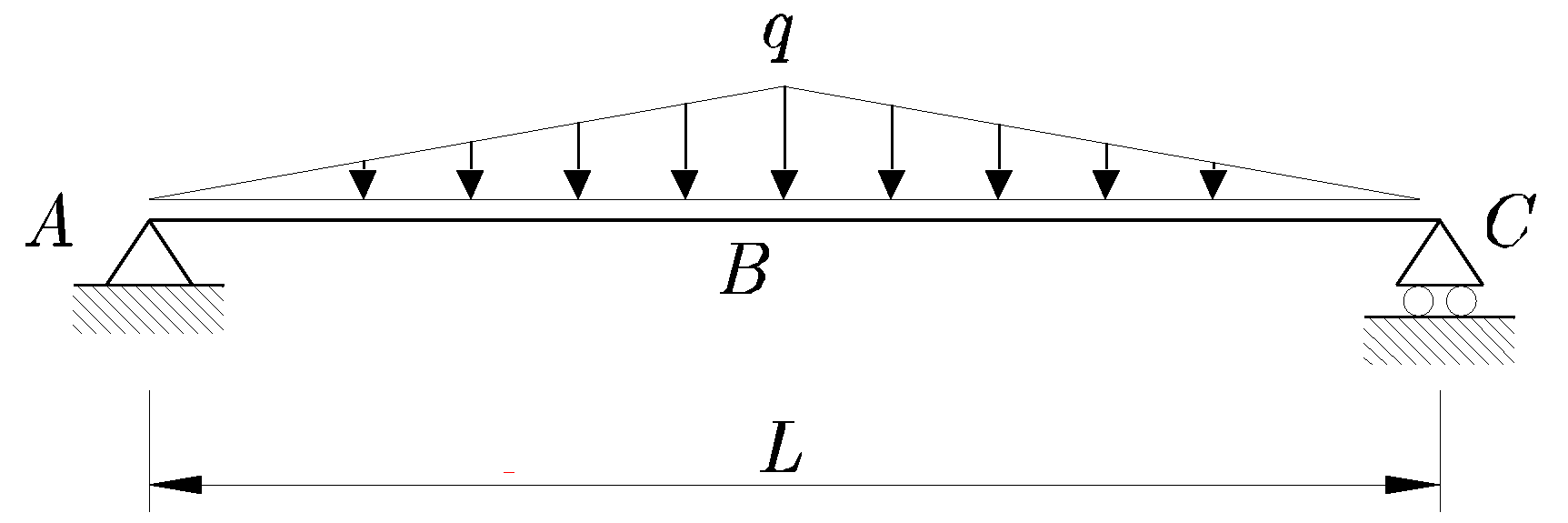Image 3-DFlexion-ejercicio

Obtener, utilizando los teoremas de Mohr:

  1. El desplazamiento vertical del punto B
  2. Los giros de los puntos A y C
  3. La deforma aproximada de la estructura

Datos:


$\displaystyle L$ $\displaystyle =$ $\displaystyle 4$    m  
$\displaystyle I_y$ $\displaystyle =$ $\displaystyle 5,5\cdot 10^{-4}$    mm$\displaystyle ^4$  
$\displaystyle q$ $\displaystyle =$ $\displaystyle 15$    kN/m  
$\displaystyle E$ $\displaystyle =$ $\displaystyle 20$    GPa  

Solución:

  1. El desplazamiento vertical del punto B

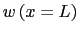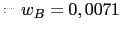    $\displaystyle w\left(x=L\right)$ $\displaystyle = w_B=0,0071$    m      

  2. Los giros de los puntos A y C

    $\displaystyle w'\left(x=0\right)$ $\displaystyle = w'_A=0,00444$    radianes      
    $\displaystyle w'\left(x=0\right)$ $\displaystyle = w'_C=-0,00444$    radianes      

  3. La deforma aproximada de la estructura

    Figura 13.10: Viga biapoyada con cargas triangulares simétricas. Deformada aproximada
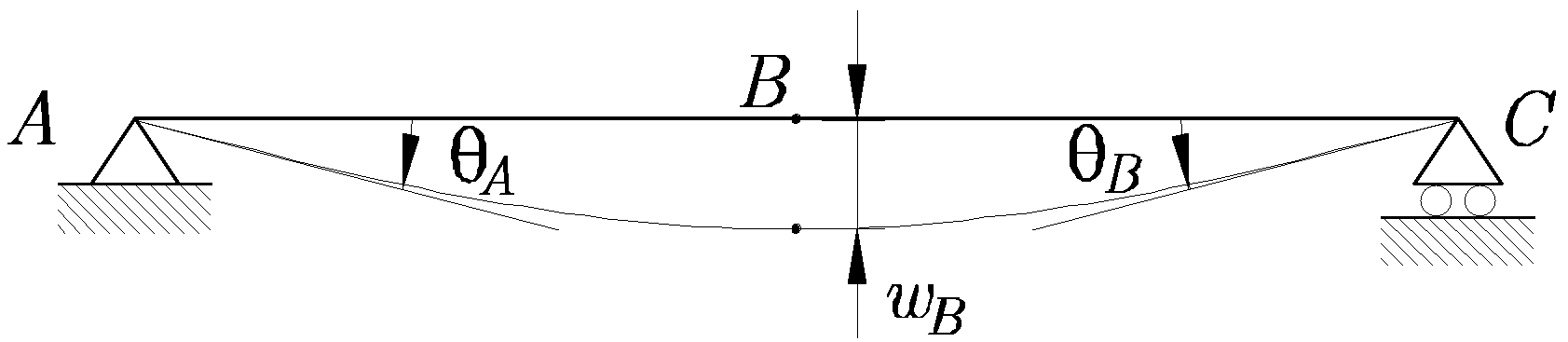    Image 4-DFlexion-ejercicio

Ejercicio 3

Para la viga de la Figura 13.11

Figura 13.11: Viga continua con doble rótula y carga uniformemente distribuida
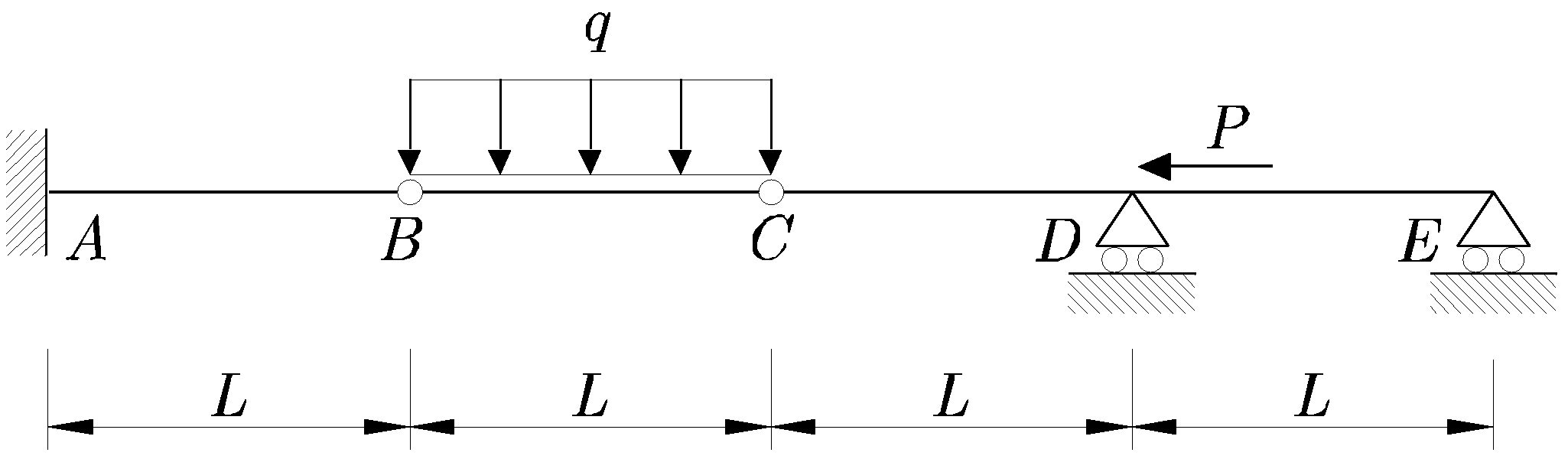Image 5-DFlexion-ejercicio

Obtener, utilizando el Principio de las Fuerzas Virtuales:

  1. Los desplazamientos verticales de los puntos B y C
  2. Los giros de los puntos D y E
  3. La deforma aproximada de la estructura

Datos:


$\displaystyle L$ $\displaystyle =$ $\displaystyle 2,5$    m  
$\displaystyle I_y$ $\displaystyle =$ $\displaystyle 5,5\cdot 10^{-4}$    mm$\displaystyle ^4$  
$\displaystyle P$ $\displaystyle =$ $\displaystyle 50$    kN   ,$\displaystyle \hspace{2mm} q = 15$    kN/m  
$\displaystyle E$ $\displaystyle =$ $\displaystyle 20$    GPa  

Solución:

  1. Los desplazamientos verticales de los puntos B y C

    $\displaystyle w\left(x=L\right)$ $\displaystyle = w_B=0,00888$    m      
    $\displaystyle w\left(x=2L\right)$ $\displaystyle = w_C=0,01776$    m      

  2. Los giros de los puntos D y E

    $\displaystyle w'\left(x=3L\right)$ $\displaystyle = w'_D=-0,00355$    radianes      
    $\displaystyle w'\left(x=4L\right)$ $\displaystyle = w'_E= 0,00177$    radianes      

  3. La deforma aproximada de la estructura

    Figura 13.12: Viga continua con doble rótula y carga uniformemente distribuida. Deformada aproximada
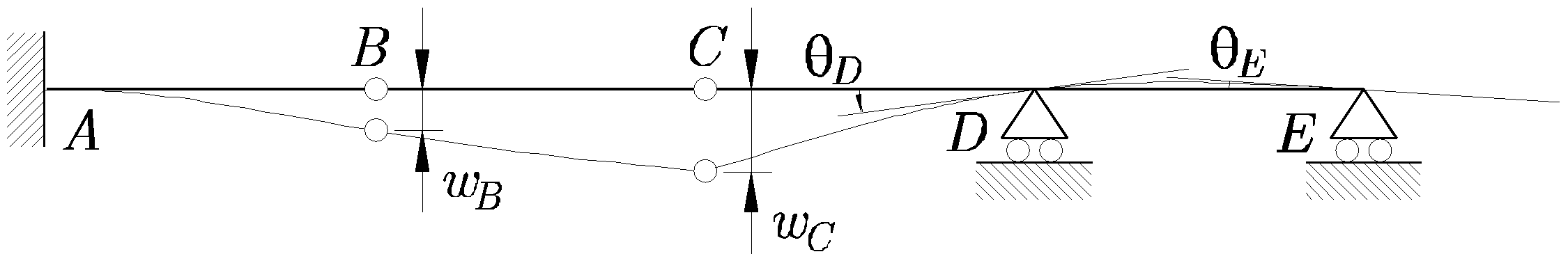    Image 6-DFlexion-ejercicio