Ejercicio 1
La sección transversal de la viga en T que se muestra en la Figura 10.7, está sometida a flexión compuesta desviada.
Figura 10.7:
Sección en T sometida a flexión compuesta desviada
|
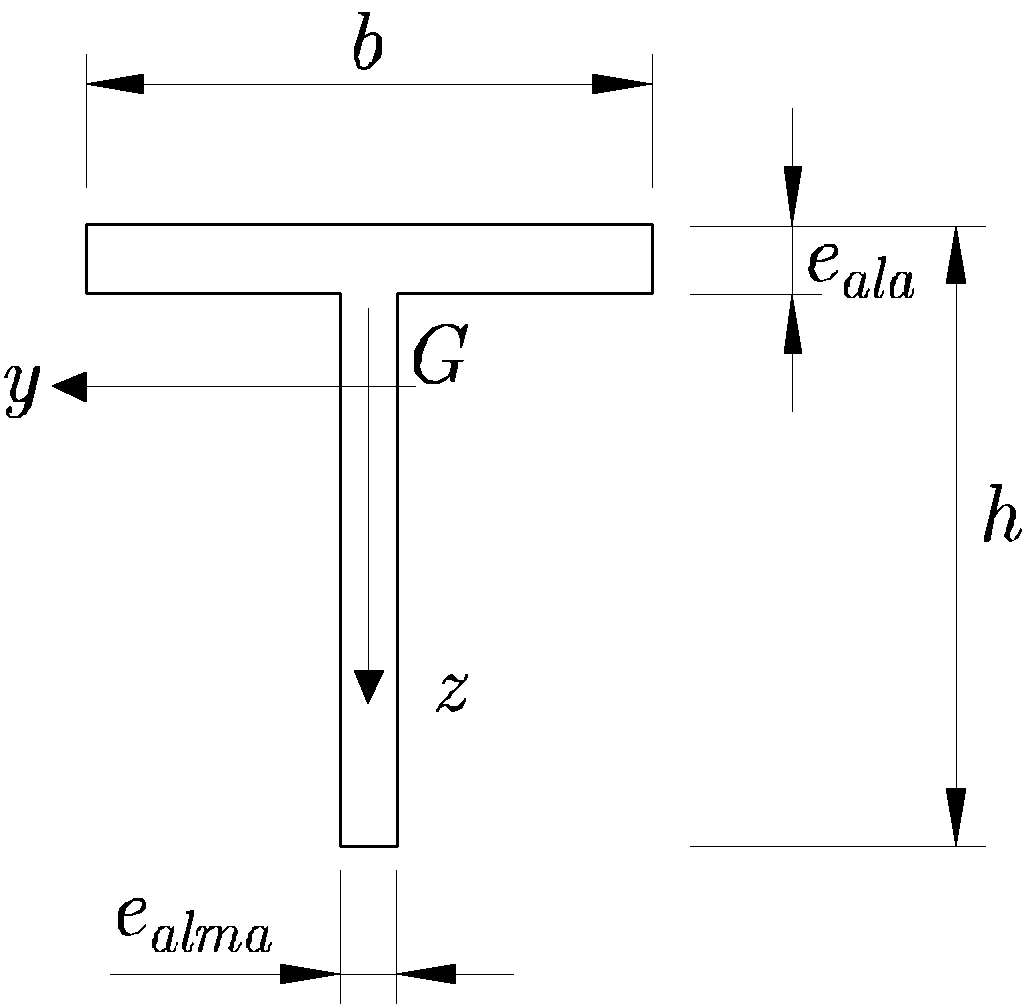 |
Obtener:
- Las propiedades estáticas de la sección: área
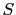 e inercias principales
e inercias principales 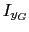 ,
, 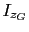
- La expresión analítica de la distribución de tensiones normales
- La ecuación del eje neutro
- La representación gráfica de la distribución de tensiones normales
Datos:
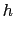 |
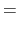 |
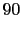 mm , mm ,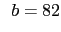 mm , mm ,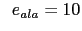 mm , mm ,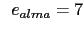 mm mm |
|
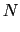 |
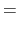 |
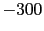 kN , kN ,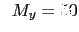 kN·m , kN·m ,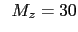 kN·m kN·m |
|
Solución:
- Las propiedades estáticas de la sección: área
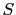 e inercias principales
e inercias principales 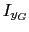 ,
, 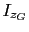
- La expresión analítica de la distribución de tensiones normales
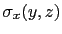 |
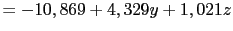 (Fuerzas en N y longitudes en mm) (Fuerzas en N y longitudes en mm) |
|
|
- La ecuación del eje neutro
- La representación gráfica del eje neutro y de la distribución de tensiones normales
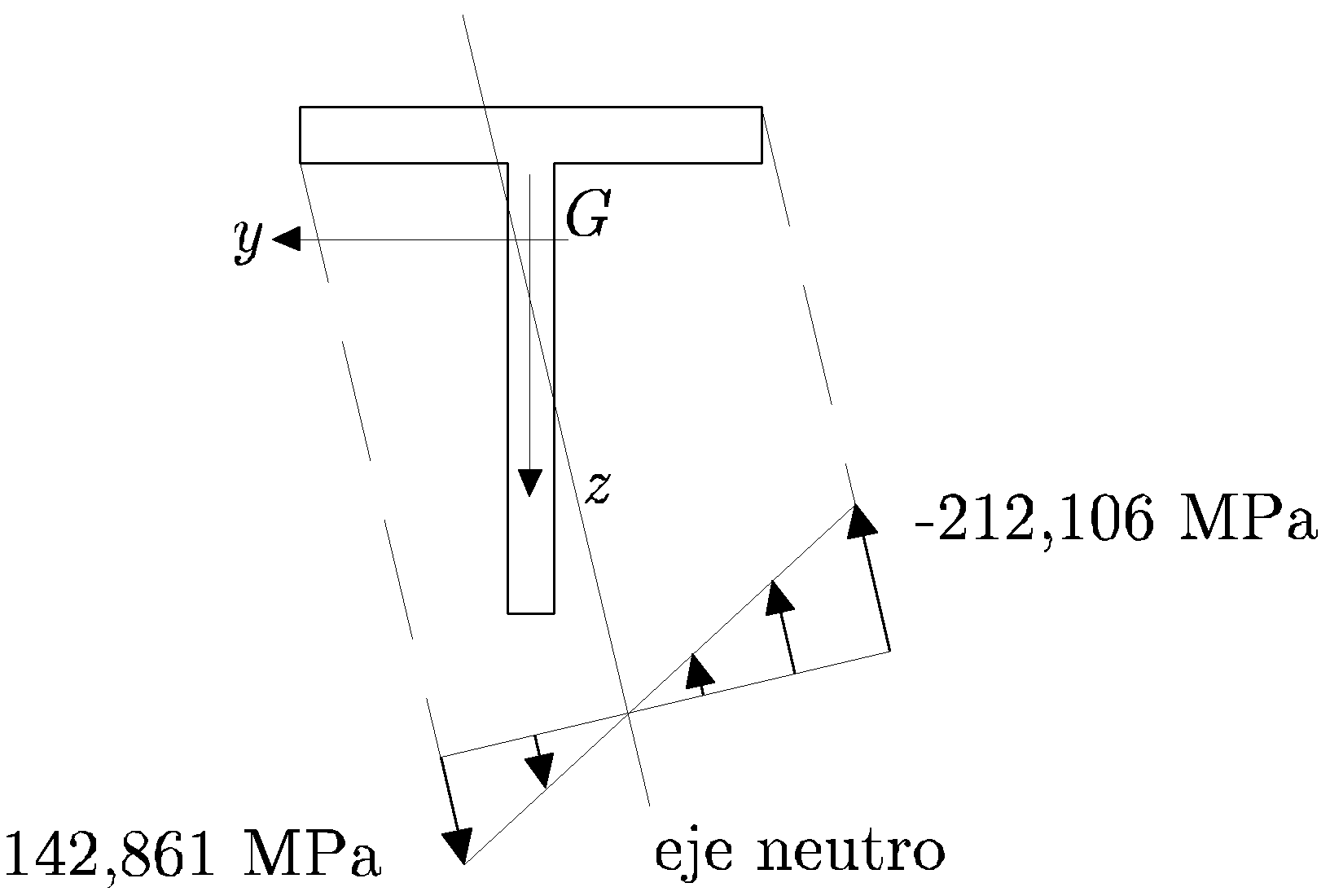
Figura 10.8:
Sección en T sometida a flexión compuesta desviada. Distribución de tensiones normales
|
 |
Ejercicio 2
Para la sección transversal de la Figura 10.9
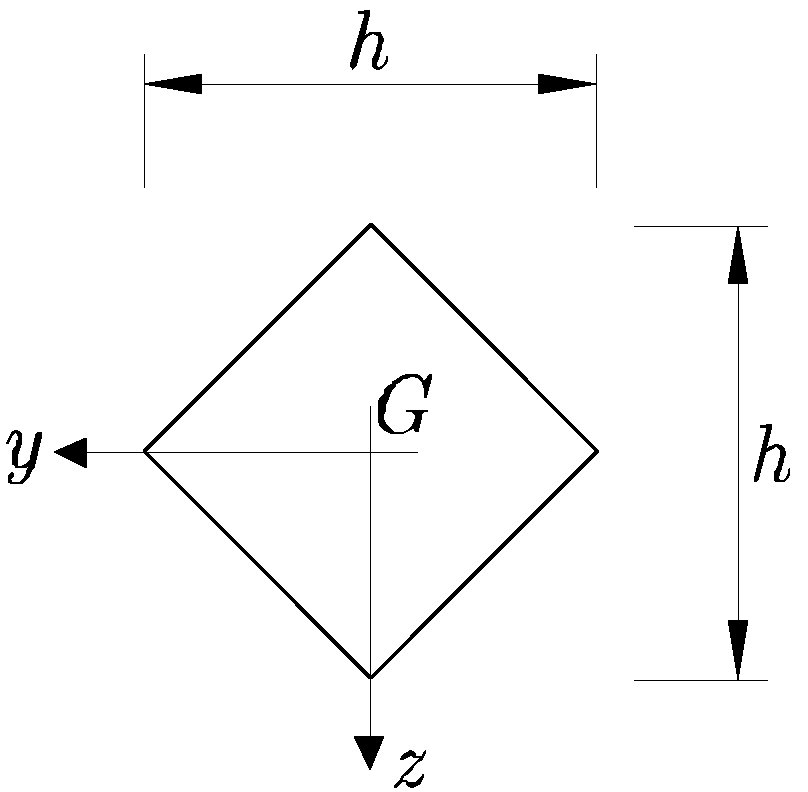
Figura 10.9:
Sección romboidal
|
 |
Obtener:
- Las propiedades estáticas de la sección: área
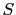 e inercias principales
e inercias principales 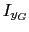 ,
, 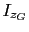
- El núcleo central de la sección
Solución:
- Las propiedades estáticas de la sección: área
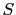 e inercias principales
e inercias principales 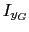 ,
, 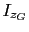
- El núcleo central de la sección
Tabla 10.1:
Coordenadas de los vértices del núcleo central de la sección
| Vértice |
Coordenadas |
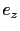 |
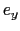 |
| 1 |
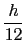 |
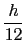
|
| 2 |
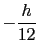 |
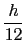
|
| 3 |
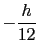 |
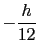
|
| 4 |
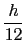 |
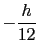 |
| |
|
|
Figura 10.10:
Sección romboidal. Núcleo central
|
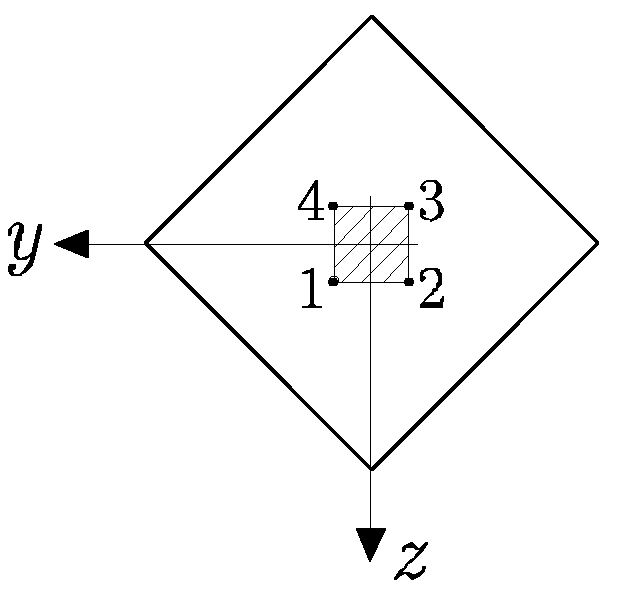 |
Ejercicio 3
En la Figura 10.11 se muestra una sección transversal rectangular, sometida a un axil de compresión excéntrico. Se admitirá que la resistencia del material a tracción es nula.
Figura 10.11:
Sección rectangular sometida a un axil de compresión excéntrico
|
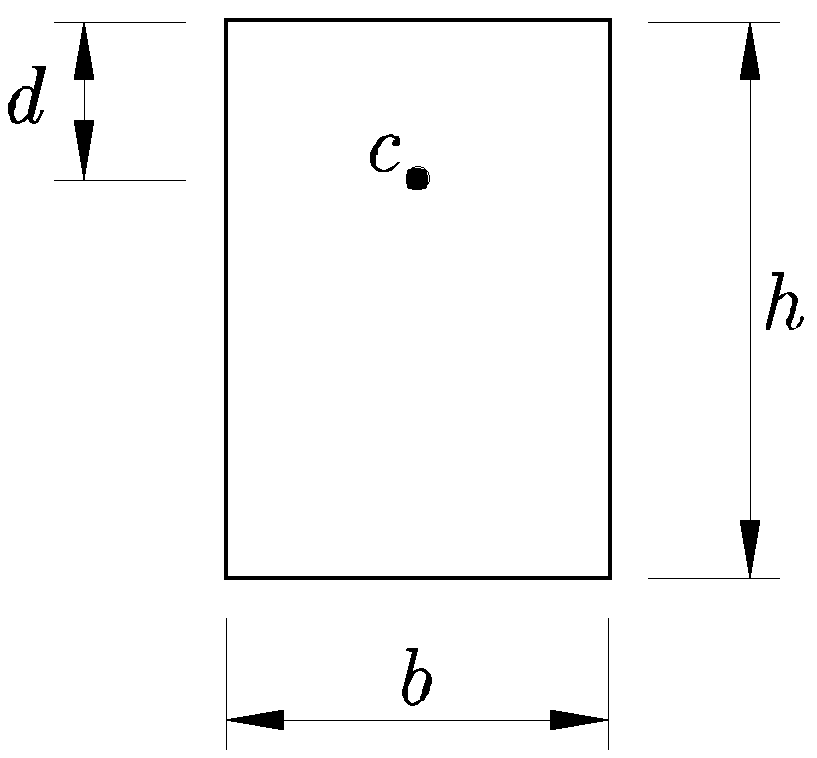 |
Obtener:
- La distancia d del punto C de aplicación del axil a la cara superior de la sección para que ésta esté comprimida
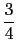 del canto h
del canto h
Solución:
- La distancia d del punto C de aplicación del axil a la cara superior de la sección para que ésta esté comprimida
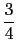 del canto h
del canto h
