Calculo gráfico de las componentes intrínsecas del vector deformación para una dirección dada

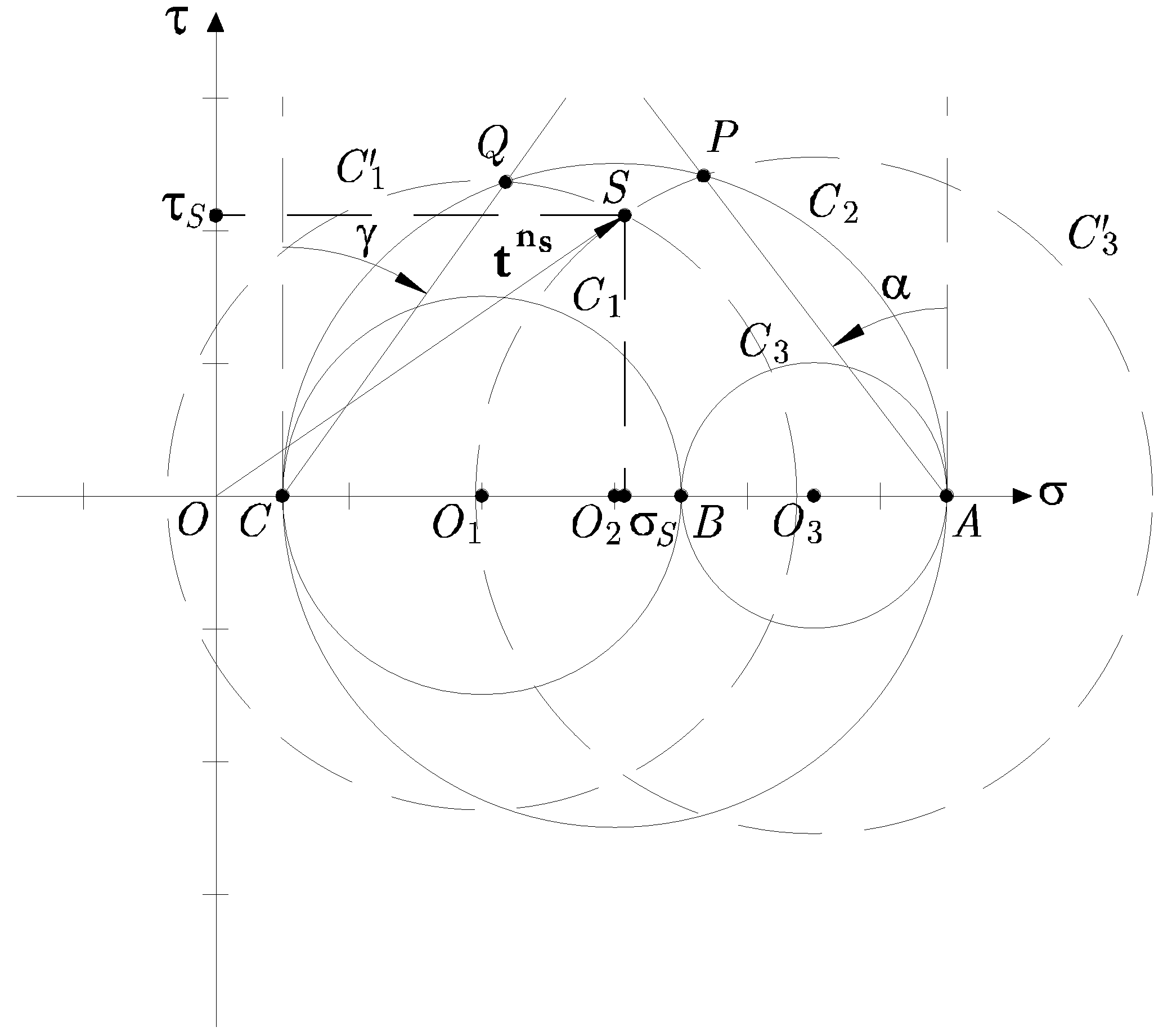
Para resolver el problema gráficamente es necesario que tanto el tensor de tensiones como el vector que define la dirección en la que se van a determinar las componentes intrínsecas, estén referidos al sistema de ejes principales. Además, dicho vector debe ser unitario. La Figura 3.18 muestra el método gráfico, que consiste en los siguientes pasos:

  1. Construcción de los círculos de Mohr como se indicó en el apartado anterior (el punto correspondiente a las componentes intrínsecas debe ser exterior a las circunferencias primera y tercera, e interior a la segunda, o bien, se hallará en alguna de las tres).
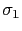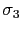  2. Usando los datos de l y n, se trazan por los puntos correspondientes a $ \sigma_1$ y $ \sigma_3$ del eje de abscisas, las rectas inclinadas mostradas en la Figura 3.18, cuyos ángulos con la dirección del eje de ordenadas son, respectivamente
    $\displaystyle \alpha= \arccos l$      
    $\displaystyle \gamma= \arccos n$      

    Estas rectas cortan a la circunferencia 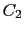$ C_2$ en los puntos P y Q
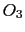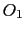  3. Por los puntos de corte P y Q se trazan sendas circunferencias con centros en $ O_3$ y $ O_1$, respectivamente.
  4. El punto S de intersección de ambas circunferencias es el extremo del vector tensión buscado. Sus proyecciones sobre el sistema 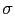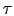$ \sigma $-$ \tau$ son las componentes intrínsecas

Figura 3.18: Construcción de los círculos de Mohr de un estado general de tensiones
Image 18-Tensiones