Criterio de rotura de Mohr para materiales frágiles sujetos a un estado plano de tensiones

El criterio de rotura de la máxima componente de la tensión normal es válido para materiales con el mismo comportamiento en tracción y compresión uniaxial. Sin embargo, hay materiales como el hormigón, la fundición, las rocas, los suelos, cuyos comportamientos en tracción y en compresión uniaxial, son diferentes . Otto Mohr propuso un criterio de rotura para estos materiales, válido para estados planos de tensiones. Este criterio precisa de realizar diferentes ensayos mecánicos en el material en estudio.

Sea un material frágil sometido a un estado plano de tensiones. En la Figura 5.8 a) se muestra la gráfica tensión-deformación correspondiente al ensayo de tracción de una probeta de dicho material. En la Figura 5.8 b) se muestran los círculos de Mohr correspondientes a los estados de tensiones definidos por los puntos A, B y U del diagrama tensión-deformación. La probeta se considera segura para niveles de fuerzas que causen tensiones inferiores a $ \sigma_1^A$ o $ \sigma_1^B$. La probeta fallará cuando la fuerza alcance el valor correspondiente a la tensión $ \sigma _e$. En la Figura 5.8 b) se comprueba como los círculos de Mohr correspondientes a estados tensionales seguros son interiores al círculo de Mohr correspondiente al estado último de tensiones.

Figura 5.8: Círculos de Mohr para los puntos de un sólido sometido a tracción uniaxial
Image 08-Plasticidad

Sea ahora un sólido hecho de un material frágil del que se conocen las tensiones últimas en tracción y compresión uniaxial. En la Figura 5.9 a) se muestran los círculos de Mohr correspondientes a estos estados. El sólido está sujeto a cargas que inducen estados planos de tensiones cuyas tensiones principales son $ \sigma_1$ y $ \sigma_2$, ambas de tracción o de compresión. Según establece Mohr, el sólido bajo el estado de cargas supuesto es seguro cuando los círculos de Mohr correspondientes a los distintos estados tensionales de cada punto del sólido, son interiores a los círculos de Mohr correspondientes a los estados últimos en tracción o compresión. Si alguna de las tensiones principales es igual a la tensión última del material en tracción o compresión uniaxial, es inseguro.

Figura 5.9: Estados tensionales seguros e inseguros de acuerdo con el criterio de rotura de Mohr
Image 09-Plasticidad

En la Figura 5.9 a) se muestran los círculos de Mohr para estados tensionales seguros y no seguros, de acuerdo con el criterio de Morh. En la Figura 5.9 b) se muestra, en el plano de las tensiones principales, el criterio de Mohr para el sólido considerado.

Para utilizar el criterio de Mohr, es necesario realizar diferentes ensayos bajo diferentes estados de carga y construir los círculo de Mohr correspondientes a los estados últimos de tensiones. Por ejemplo, realizando ensayos de compresión uniaxial, torsión pura y tracción uniaxial en un material, se pueden construir los círculos de Mohr correspondientes a los estados últimos de tensiones dados por estos ensayos, así como trazar la envolvente de dichos círculos, tal como se muestra en la Figura 5.10 a). Según el criterio de rotura de Mohr, un sólido hecho del mismo material que la probeta ensayada, sometido a un estado plano de tensiones, es seguro si el círculo de Morh correspondiente a cualquier estado tensional posible en el sólido es interior a la envolvente definida anteriormente. En la Figura 5.10 b) se muestra el criterio en el espacio de tensiones principales.

Figura 5.10: Envolvente de fallo para un estado plano de tensiones de acuerdo con el criterio de rotura de Mohr
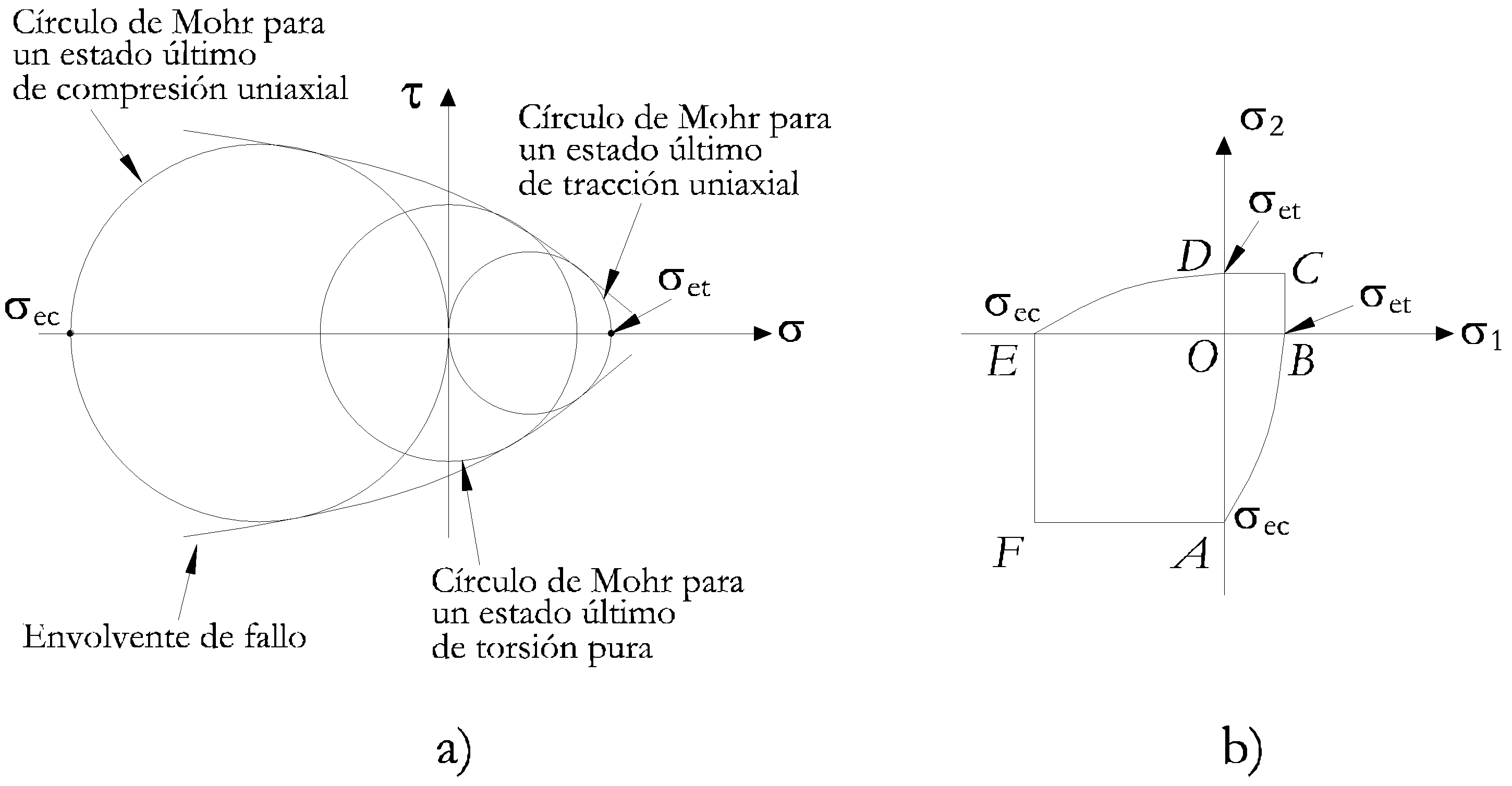Image 10-Plasticidad

Si para un determinado material solamente se dispone de los círculos de Mohr correspondientes a los estados últimos tensionales de tracción y compresión uniaxial, como se muestra en la Figura 5.11 a), la envolvente de Mohr puede aproximarse por rectas tangentes a dichos círculos. El correspondiente criterio de rotura en el plano de tensiones principales se muestra en la Figura 5.11 b).

Figura 5.11: Envolvente de fallo simplificada para un estado plano de tensiones de acuerdo con el criterio de rotura de Mohr
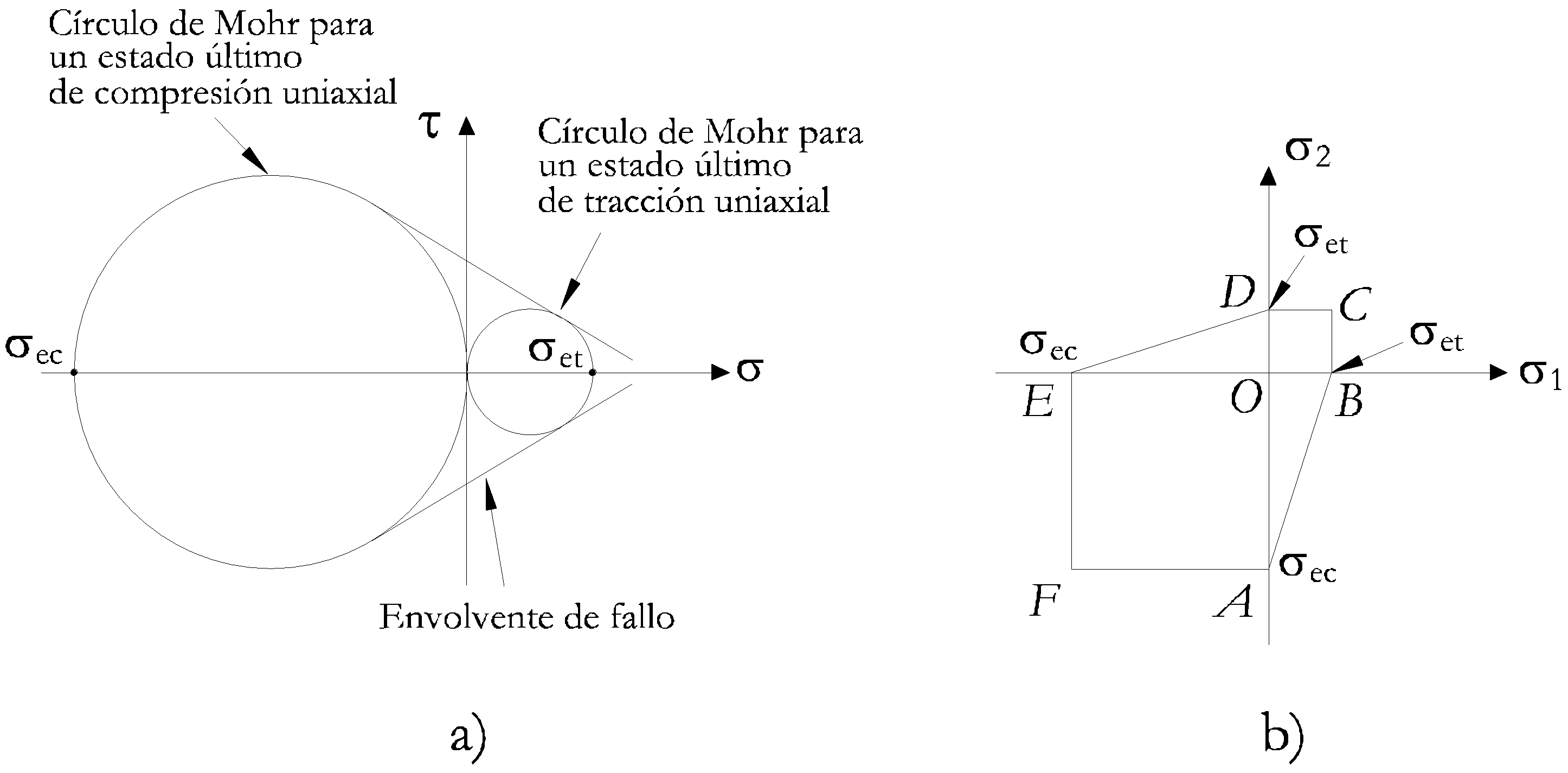Image 11-Plasticidad

Por tanto, el criterio de rotura de Mohr puede enunciarse como sigue: un sólido sometido a un estado plano de tensiones rompe cuando las cargas actuantes alcanzan un valor tal que el punto representativo del estado tensional caiga sobre el contorno definido por ABCDEFA de los criterios de rotura mostrados en la Figura 5.10 b) y en la Figura 5.11 b).

Para materiales cuyas propiedades en tracción y compresión uniaxial sean las mismas, la geometría del criterio de Mohr es similar a la dada por el criterio de Tresca.

En la mayoría de los materiales cohesivos, como el hormigón, suelos o rocas, el criterio de rotura depende de la presión hidrostática. De forma que un incremento en la presión hidrostática de compresión produce un incremento en la capacidad del material de resistir las tensiones solicitadas sin romper. Es decir, se admite que la existencia de una presión hidrostática actuando sobre dichos materiales no provoca rotura de los mismos.