Solución gráfica para tensiones sobre un plano inclinado

Si se conocen las tensiones 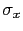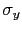$ \sigma_x$, $ \sigma_y$ y $ \tau_{xy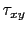}$ en un sistema 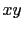$ xy$, las tensiones 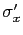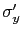$ \sigma'_x$, $ \sigma'_y$ y $ \tau'_{xy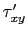}$ en cualquier plano inclinado que forme un ángulo 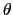$ \theta$ con la dirección positiva del eje x, pueden obtenerse gráficamente siguiendo el procedimiento que se muestra en la Figura 3.15 como sigue:

Figura 3.15: Solución gráfica para tensiones sobre un plano inclinado
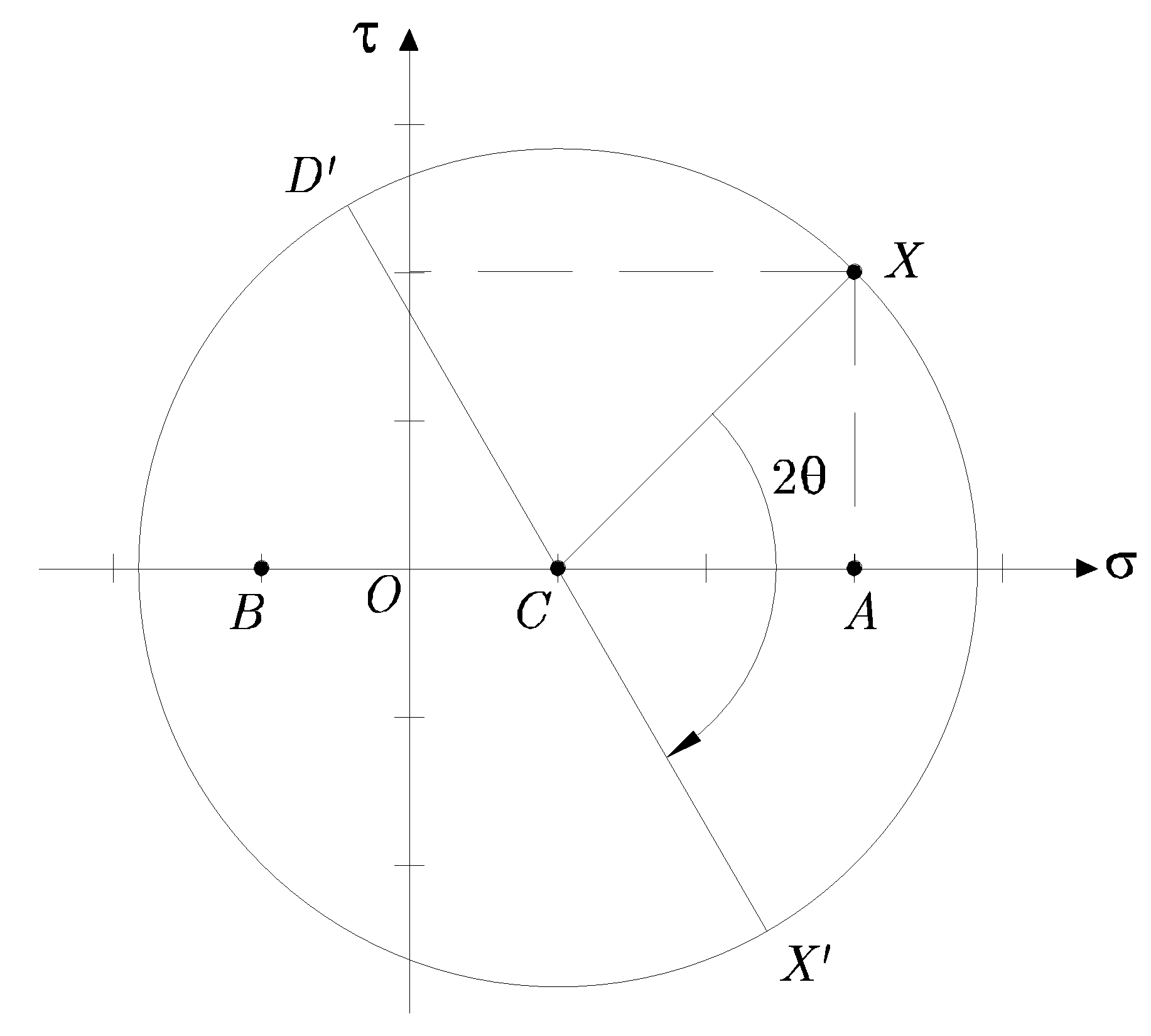Image 15-Tensiones

  1. Se traza el círculo de Mohr según se ha descrito en el apartado anterior.
  2. Para encontrar el punto sobre la circunferencia de Mohr que represente un plano en el cuerpo elástico cuya normal está girada un ángulo 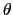$ \theta$ (en sentido antihorario) respecto del eje 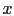$ x$, hay que girar un ángulo 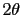$ 2\theta$ (en sentido horario) a partir de la línea 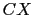$ CX$. 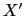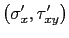El punto $ X'$ de intersección de la recta girada con la circunferencia es el punto buscado, cuyas coordenadas son $ \left(\sigma'_x, \tau'_{xy}\right)$.
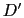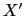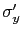  3. La abscisa del punto $ D'$, que está en el extremo opuesto del diámetro que pasa por $ X'$ es $ \sigma'_y$, siendo las coordenadas del punto 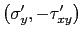$ \left(\sigma'_y, -\tau'_{xy}\right)$.