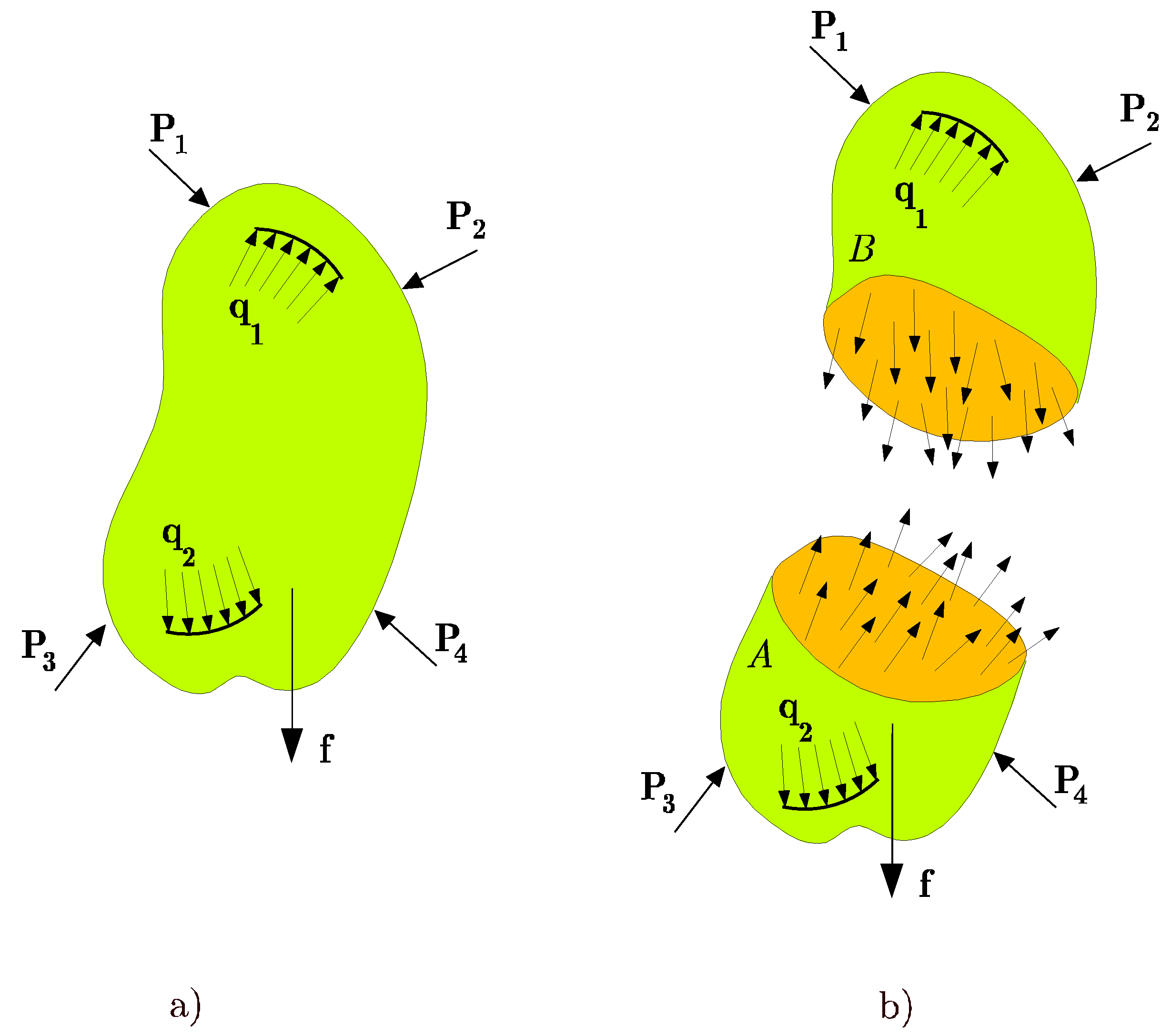 |
Al deformarse un sólido bajo la acción de unas cargas, la variación relativa de la distancia entre las partículas que lo constituyen no es indefinida debido a la acción de las fuerzas de atracción intermoleculares, a excepción de que se produzca la rotura del sólido.
Sea un sólido en equilibrio sometido a un sistema de fuerzas exteriores y a fuerzas por unidad de masa como se muestra en la Figura 3.1 a). Mediante un corte imaginario a dicho sólido por una superficie arbitraria, como el que se muestra en la Figura 3.1 b), se aisla un trozo de sólido. En el interior del sólido actúan las fuerzas por unidad de masa correspondientes. En el contorno actúan fuerzas por unidad de superficie que en la superficie de corte corresponden a la acción de cada una de las dos partes en que se divide el sólido sobre la otra. Por equilibrio, ambos conjuntos de fuerzas por unidad de superficie han de ser iguales y de sentidos contrarios.
Estas fuerzas por unidad de superficie no son fuerzas actuantes sobre el exterior del sólido. Son fuerzas internas y resultantes a nivel macroscópico de las fuerzas intermoleculares que se oponen a las separaciones entre moléculas del sólido. No obstante, tanto las fuerzas por unidad de superficie que actúan en el exterior del sólido como estas fuerzas internas, tienen el mismo sentido físico: son fuerzas actuantes por unidad de superficie. Cada una de estas fuerzas recibe el nombre de vector tensión y se denota como
![]() .
.
En el contorno exterior del sólido, la superficie sobre la que actúan las fuerzas exteriores está perfectamente definida en cada punto del mismo (el vector normal al contorno en dicho punto es único) y la tensión es una función de punto
![]() . Sin embargo, para caracterizar el vector tensión en un punto interior del sólido es necesario indicar el plano de corte, tangente a dicho punto, utilizado. Este plano queda definido si se conoce su normal
. Sin embargo, para caracterizar el vector tensión en un punto interior del sólido es necesario indicar el plano de corte, tangente a dicho punto, utilizado. Este plano queda definido si se conoce su normal
![]() . Es pues una hipótesis aceptable considerar que el vector tensión asociado a un punto interior de un sólido elástico depende del punto considerado y de la normal en tal punto al plano tangente considerado
. Es pues una hipótesis aceptable considerar que el vector tensión asociado a un punto interior de un sólido elástico depende del punto considerado y de la normal en tal punto al plano tangente considerado
![]() . Ya que por un punto pasan infinitos planos, habrá infinitos vectores tensión asociados a un mismo punto. Cabe preguntarse ¿cómo es posible sacar conclusiones sobre el estado tensional en cualquier punto de un sólido, si la magnitud que lo define varía según el plano que se considere? ¿Existe alguna relación que ligue estos infinitos vectores tensión? En el desarrollo del tema se responderán estas cuestiones.
. Ya que por un punto pasan infinitos planos, habrá infinitos vectores tensión asociados a un mismo punto. Cabe preguntarse ¿cómo es posible sacar conclusiones sobre el estado tensional en cualquier punto de un sólido, si la magnitud que lo define varía según el plano que se considere? ¿Existe alguna relación que ligue estos infinitos vectores tensión? En el desarrollo del tema se responderán estas cuestiones.