Concepto de deformación

Las partículas que constituyen cualquier sólido real, bajo la acción de cargas que actúan sobre él, varían su posición en el espacio. Por consiguiente, el sólido adopta una configuración deformada distinta de la inicial.

Figura 2.1: Concepto de deformación
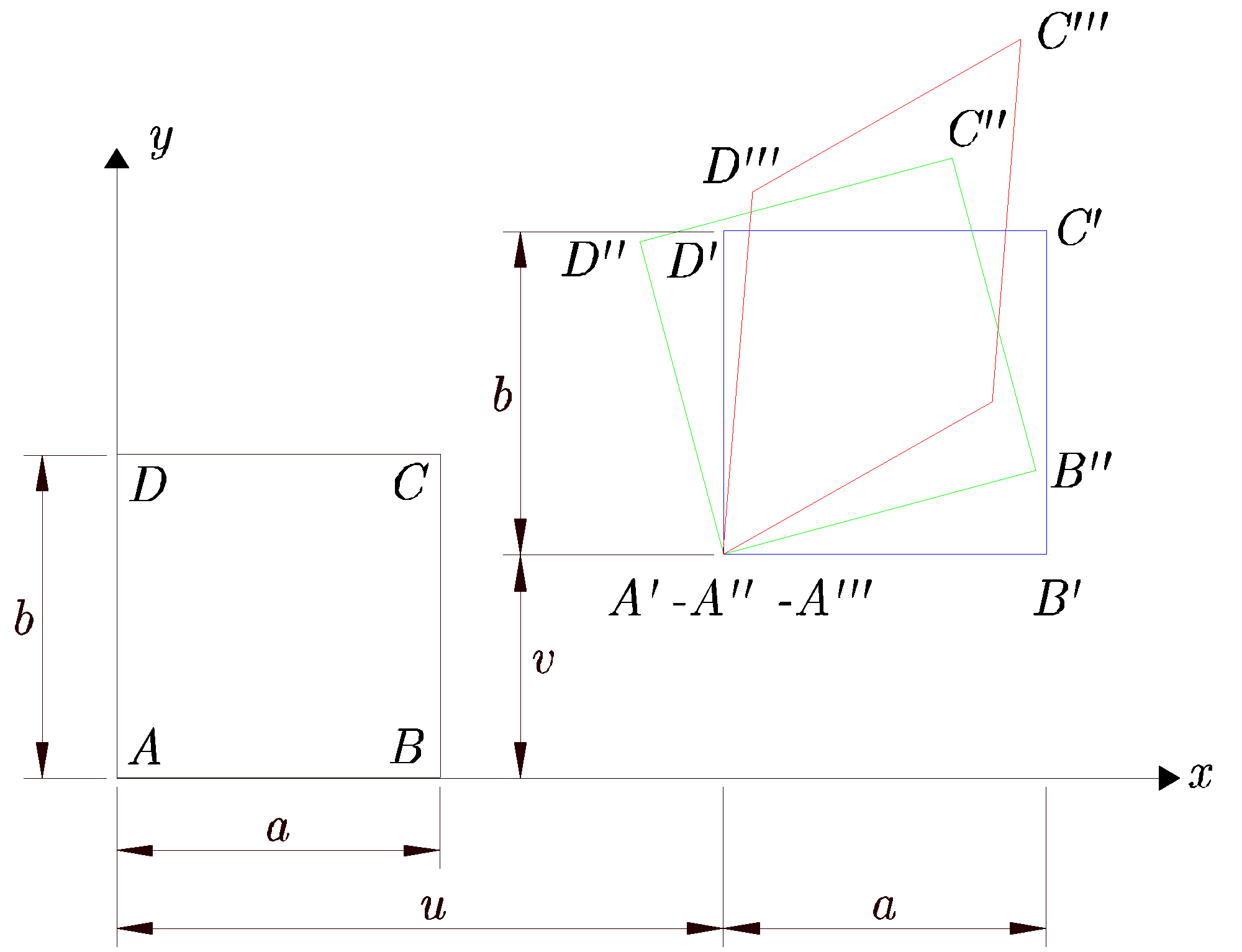
Image 01-Deformaciones

Existe deformación en un sólido si se produce un desplazamiento relativo entre las partículas que lo constituyen. El desplazamiento de los puntos de un sólido es debido a dos componentes: una componente de movimiento como sólido rígido y otra de deformación. Así pues, el desplazamiento de los puntos de un sólido no implica necesariamente que éste se deforme. El rectángulo $ ABCD$ de la Figura 2.1 se desplaza hacia otra posición $ A'B'C'D'$, pero es idéntico al inicial; es decir, no se ha producido ningún acercamiento o separación entre sus partículas, o lo que es lo mismo, no se ha producido ninguna deformación. Solamente se ha producido un movimiento como cuerpo rígido. Lo mismo ocurre al pasar a la posición $ A''B''C''D''$ mediante una rotación como sólido rígido. Finalmente, cuando el rectángulo pasa a la posición $ A'''B'''C'''D'''$, sí que se deforma.

Los dos casos más simples de deformación son el alargamiento unitario y la deformación tangencial. Un ejemplo de estos tipos de deformación se muestra en la Figura 2.2.

Figura 2.2: Ejemplos de deformación: a) alargamiento en la dirección $ x$, b) alargamiento en la dirección $ y$, y c) deformación tangencial pura sin rotación
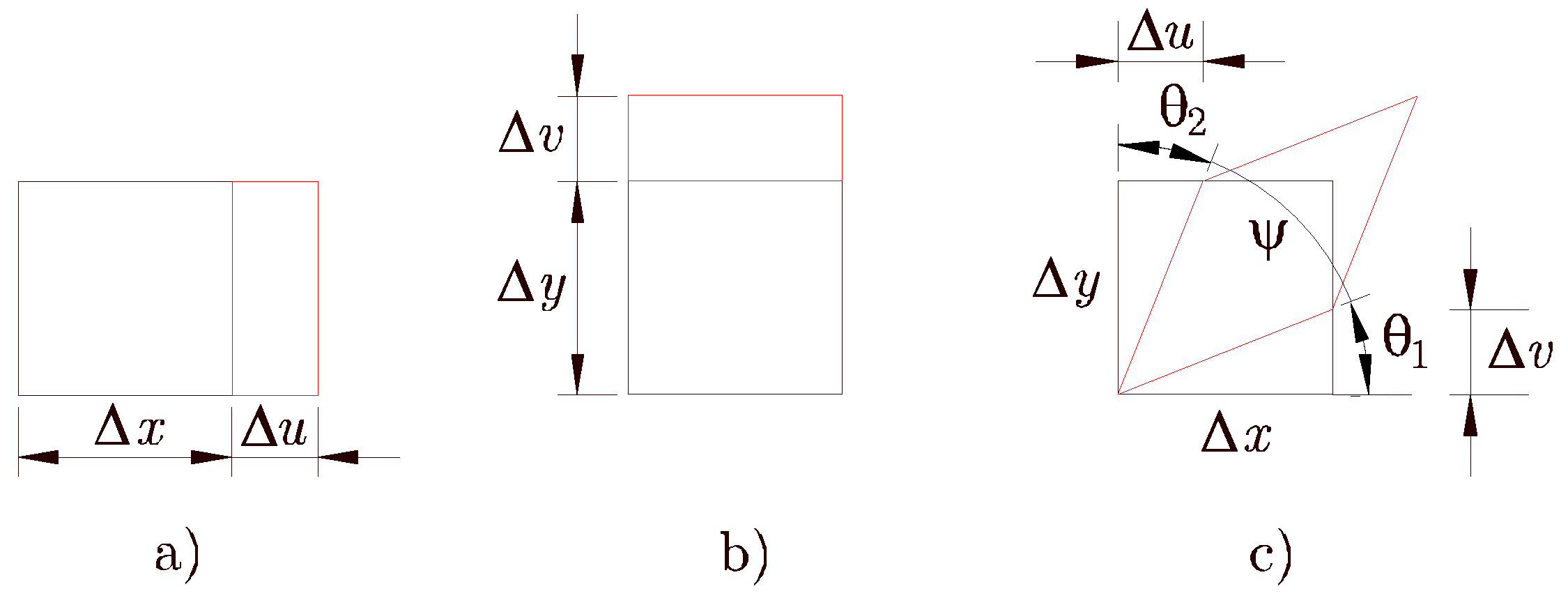Image 02-Deformaciones

El alargamiento unitario se define como un cambio de longitud por unidad de longitud. Se denomina $ \varepsilon$, indicando por medio de un subíndice la dirección del alargamiento. Observando las Figuras 2.2 a) y 2.2 b), se deduce que

$\displaystyle \varepsilon_x\simeq\displaystyle\frac{\Delta u}{\Delta x}$   ,$\displaystyle \hspace{2mm} \varepsilon_y\simeq\displaystyle\frac{\Delta v}{\Delta y}$ (2.1)

La deformación tangencial se define como la mitad del decremento del ángulo recto que forman inicialmente dos segmentos infinitamente pequeños. En referencia a la Figura 2.2 c), la expresión de la deformación tangencial es


$\displaystyle \gamma_{xy}\simeq\displaystyle\frac{\pi}{2} - \psi=\theta_1+\theta_2$     (2.2)
$\displaystyle \varepsilon_{xy}\simeq\displaystyle\frac{1}{2}\gamma_{xy}\simeq\d... ...laystyle\frac{\Delta u}{\Delta y}+\displaystyle\frac{\Delta v}{\Delta x}\right)$     (2.3)

Cuando $ x$ e $ y$ tienden a cero, las expresiones (2.1) y (2.3) toman la forma

$\displaystyle \varepsilon_x=\displaystyle\frac{\partial u}{\partial x}$   ,$\displaystyle \hspace{2mm} \varepsilon_y=\displaystyle\frac{\partial v}{\partial y}$   ,$\displaystyle \hspace{2mm} \varepsilon_{xy}=\displaystyle\frac{1}{2}\gamma_{xy... ...\frac{\partial u}{\partial y}+\displaystyle\frac{\partial v}{\partial x}\right)$ (2.4)

donde $ u$ y $ v$ son las componentes del desplazamiento en dirección de los ejes $ x$ e $ y$, respectivamente.

Para obtener la expresión de la deformación tangencial se han aproximado los ángulos por sus tangentes (hipótesis de pequeños desplazamientos). El factor $ \frac{1}{2}$ en la deformación tangencial se debe a que las componentes de la deformación son las componentes de un tensor de segundo orden simétrico. De la expresión (2.2) se deduce que la deformación tangencial es positiva si el ángulo pasa a ser agudo.