Al deducir la fórmula de Euler, se empleó la ecuación diferencial de la línea elástica que se basa en la ley de Hooke, la cual es válida mientras no se sobrepase la tensión del límite de proporcionalidad del material, ![]() hasta un valor que se denominará tensión crítica
hasta un valor que se denominará tensión crítica
![]() , es decir
, es decir
Esta tensión crítica es igual a la tensión que se produce en cualquier sección transversal de la barra al actuar la carga crítica
siendo S el área de la sección transversal de la barra.
El radio de giro ![]() de la sección transversal de una barra es
de la sección transversal de una barra es
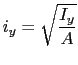 . La ecuación (15.18) puede escribirse en función del radio de giro como
. La ecuación (15.18) puede escribirse en función del radio de giro como
A la magnitud
![]() , que caracteriza la influencia de las dimensiones de la barra y las condiciones de apoyo de sus extremos, se la denomina esbeltez de la barra, es una magnitud adimensional, y se denota por
, que caracteriza la influencia de las dimensiones de la barra y las condiciones de apoyo de sus extremos, se la denomina esbeltez de la barra, es una magnitud adimensional, y se denota por ![]() . Se pueden reescribir las ecuaciones (15.16) y (15.19) en función de la esbeltez
. Se pueden reescribir las ecuaciones (15.16) y (15.19) en función de la esbeltez
Hasta ahora se ha empleado el momento de inercia correspondiente al eje y de la sección recta, al suponer sólo la posibilidad de pandeo en el plano XZ. Sin embargo, si no está impedido el movimiento, la barra puede pandear en cualquier plano. De la ecuación (15.21) se deduce que la barra pandeará en el plano de mayor esbeltez
![]() . Si las condiciones de apoyo en ambos planos son iguales, el pandeo se producirá en el plano del eje de mayor inercia de la sección recta (alrededor del eje de menor inercia).
. Si las condiciones de apoyo en ambos planos son iguales, el pandeo se producirá en el plano del eje de mayor inercia de la sección recta (alrededor del eje de menor inercia).
La validez de la fórmula de Euler planteada en la ecuación (15.17), reescrita en función de la esbeltez máxima, es
Despejando la esbeltez de la ecuación (15.22), se obtiene el valor mínimo de tener esbeltez de una barra para que se pueda aplicar la fórmula de Euler
La curva ABC de la Figura 15.9 representa la ecuación (15.23), y se denomina hipérbola de Euler.
Los pilares que pueden ser calculados a pandeo con la teoría de Euler se denominan pilares esbeltos.
Los pilares con una esbeltez máxima muy baja, pueden fallar por resistencia antes de que se alcance la tensión crítica de compresión. Los pilares con este tipo de fallo se denominan pilares cortos.
Existe una zona intermedia, en la que el cálculo no se puede realizar por compresión, puesto que la barra es suficientemente larga y mantiene en su comportamiento las particularidades relacionadas con el fenómeno de la pérdida de estabilidad, y tampoco se puede aplicar el cálculo de la estabilidad según Euler, puesto que en el material de la barra surgen deformaciones plásticas. Son los denominados pilares medios. Para tratar este tipo de pilares se han planteado diversas teorías, aunque no van a ser tratadas en este tema.