Dependencia entre la carga crítica y las condiciones de apoyo de la barra

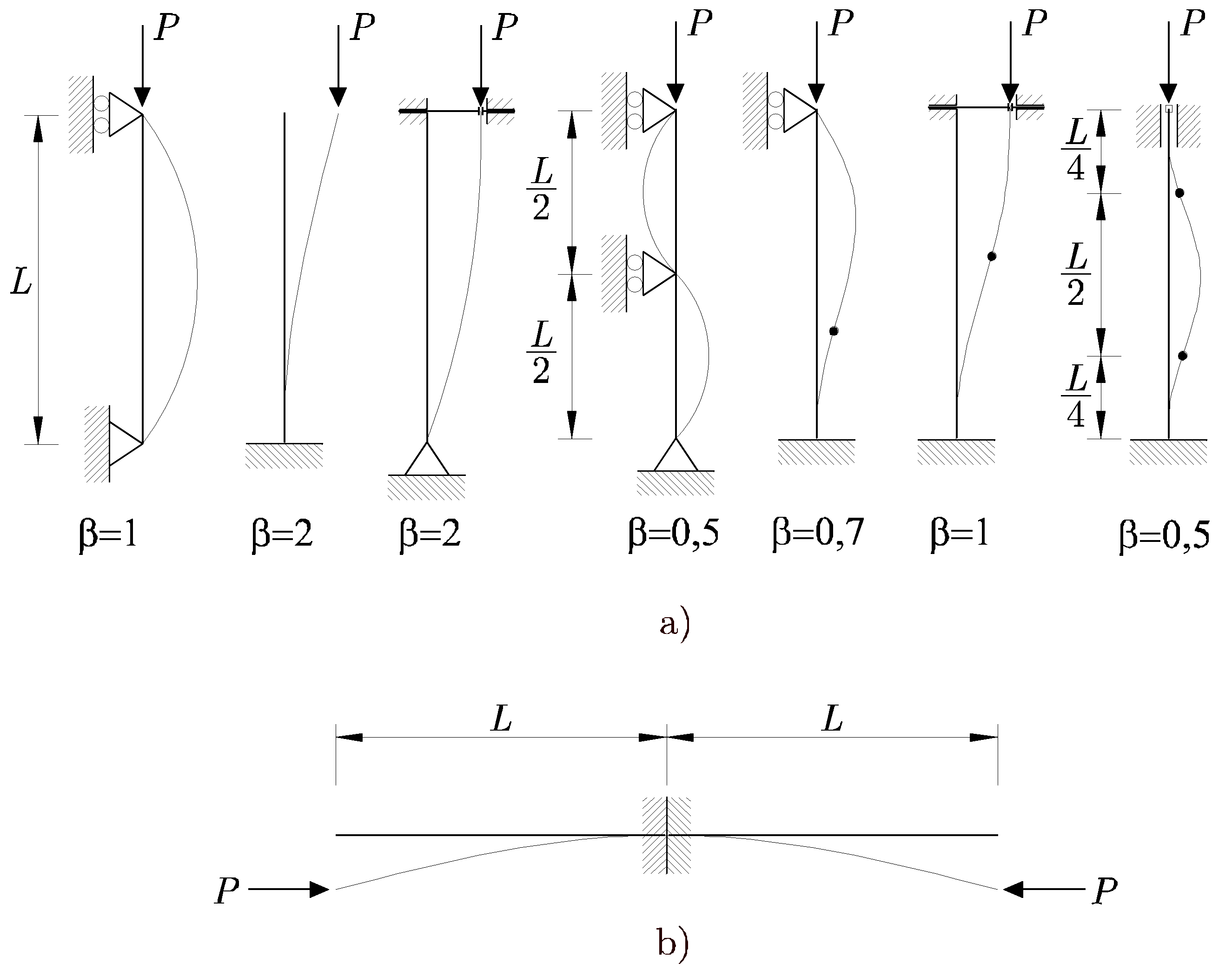
Generalmente, los extremos de la barra se apoyan de alguna de las formas representadas en la Figura 15.7.

Figura 15.7: Dependencia entre la carga crítica y las condiciones de apoyo de la barra
Image 07-Pandeo

En la barra biarticulada analizada para la deducción de la fórmula de Euler, se demostró que la flexión de ésta durante el pandeo ocurre según una semionda de sinusoide, obteniéndose la expresión de la fuerza crítica indicada en la ecuación (15.9). Se llamará al problema de Euler caso fundamental. Es posible utilizar la solución obtenida para el caso fundamental para otras condiciones de apoyo de la barra. Así, por ejemplo, si la barra se empotra en un extremo y se deja libre en el otro, la línea elástica de la barra podrá ser transformada en la línea elástica de una barra biarticulada como se indica en la Figura 15.8.

Figura 15.8: Obtención del coeficiente de esbeltez $ \beta$ de una barra empotrada-libre a partir de la barra articulada-articulada
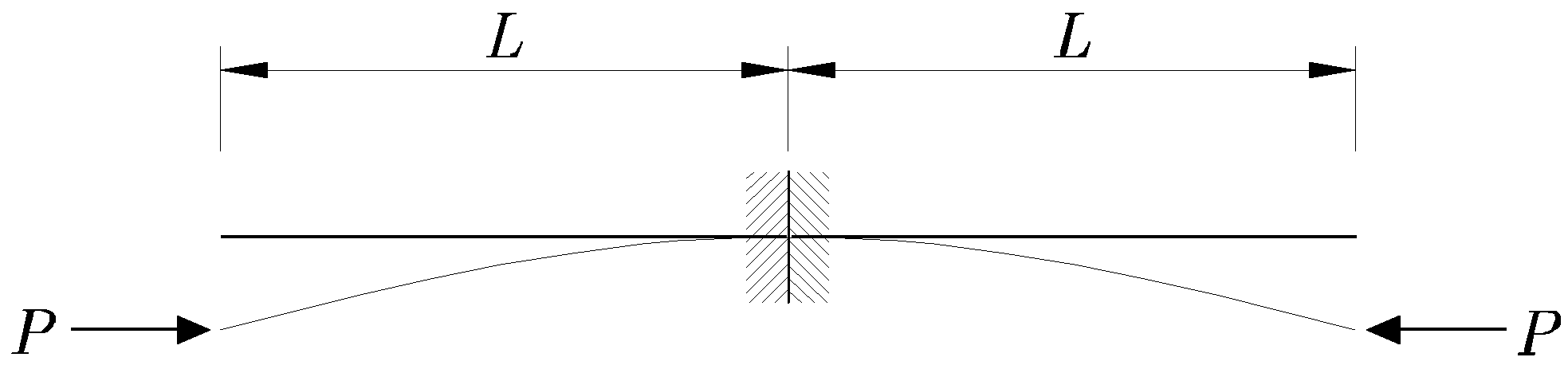Image 08-Pandeo

Observando dicha figura, se puede concluir que la carga crítica correspondiente a una barra de longitud L empotrada en un extremo, será igual a la carga crítica correspondiente al caso fundamental para una barra de longitud 2L.

$\displaystyle P_{\text{cr\'{\i}t}}=\displaystyle\frac{\pi^2EI_y}{\left(2L\right)^2}$ (15.14)

En el caso de una barra biarticulada con un apoyo en mitad de la misma, al perder la estabilidad se flexiona según dos semiondas. Es decir, cada uno de sus vanos pierde la estabilidad de la misma forma que el caso fundamental para una barra de longitud $ \displaystyle\frac{L}{2}$. Por lo tanto, la carga crítica es

$\displaystyle P_{\text{cr\'{\i}t}}=\displaystyle\frac{\pi^2EI_y}{\left(\displaystyle\frac{L}{2}\right)^2}$ (15.15)

Generalizando las ecuaciones obtenidas, se puede determinar una expresión general de la fuerza crítica para una barra comprimida, y para cualquier tipo de apoyo, como

$\displaystyle P_{\text{cr\'{\i}t}}=\displaystyle\frac{\pi^2EI_y}{\left(\beta L\right)^2}$ (15.16)

$ \beta$ es el coeficiente de esbeltez, que depende de las condiciones de apoyo de la barra. De acuerdo con lo anterior, se denomina longitud de pandeo $ L_k$ de una pieza sometida a un esfuerzo normal de compresión a la longitud que debería tener la pieza del caso fundamental, para tener la misma carga crítica que la pieza real considerada. La longitud de pandeo viene dada por la expresión $ L_k=\beta L$.

De la ecuación (15.16) se puede concluir que, cuanto menor es $ \beta$, mayor será la carga crítica y, por lo tanto, la carga admisible sobre la barra. Por ejemplo, la carga crítica de la barra empotrada en sus dos extremos es 16 veces mayor que la de la barra empotrada en un extremo y libre en el otro. Por este motivo, allí donde resulte posible, se deben empotrar rígidamente los dos extremos de la barra; sin embargo, en la práctica, esto no es siempre posible. Los elementos que sirven de apoyo de los extremos de las barras presentan, siempre, un cierto grado de elasticidad, y esto introduce cierta indeterminación en los cálculos. Por eso, muy a menudo, el cálculo se realiza considerando que los extremos están articulados, lo que va a favor de la seguridad.