Problema de Euler

El planteamiento que sigue fue hecho por el matemático L. Euler en el último tercio del siglo XVIII. Por este motivo, al hablar de estabilidad de la barra comprimida se emplean las expresiones problema de Euler o estabilidad de la barra según Euler.

En el planteamiento del problema de Euler se consideran las siguientes hipótesis:

  1. La barra es esbelta de sección constante y está constituida por un material perfectamente elástico. Se considera que no existe imperfección geométrica alguna.
  2. Los ejes y y z, son los principales de inercia.
  3. Las tensiones que se generan al comprimir la barra no superan en ningún caso el límite elástico del material. Se consideran pequeñas deformaciones y pequeños desplazamientos.
  4. El material está libre de tensiones residuales.
  5. Las cargas de compresión P aplicadas en las secciones extremas de la barra resultan de una distribución constante de tensiones normales sobre esas secciones. Esto implica que las cargas están aplicadas exactamente en el centro de gravedad y en la dirección de la directriz de la barra.

Figura: 15.4 Estabilidad de la barra de Euler
Image 04-Pandeo

Se supondrá que, por cierta causa, la barra comprimida de la Figura 15.4 recibió cierta flexión. Se van a analizar las condiciones que hacen posible el equilibrio de la barra con el eje flexionado.

Cuando se consideran pequeños desplazamientos, se verifica la ecuación

$\displaystyle E\hspace{0.5mm}I_y\hspace{0.5mm}z''=M_y$ (15.2)

La flexión de la barra ocurre en el plano XZ, por lo tanto $ I_y$ es el momento de inercia de la sección respecto a un eje perpendicular a dicho plano. El momento flector $ M_y$ es, en valor absoluto, igual a $ P\hspace{0.5mm}z$. Se considerará positivo el momento que aumenta la curvatura, luego analizando la línea elástica de la viga de la Figura 15.4, se observa que la fuerza de compresión P disminuye, en el sentido algebraico de la palabra, la curvatura. El momento de la fuerza P se orienta de tal manera que, al curvar más la línea elástica, la curvatura se hace más negativa, es decir, disminuye. Así pues,

$\displaystyle E\hspace{0.5mm}I_y\hspace{0.5mm}z''=-M_y=-P\hspace{0.5mm}z$ (15.3)

Llamando 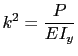$ k^2=\displaystyle\frac{P}{EI_y}$ y sustituyendo ésta expresión en la ecuación (15.3), se obtiene

$\displaystyle z''+k^2z=0$ (15.4)

Esta es una ecuación diferencial lineal de segundo orden, de coeficientes constantes (se considera que la inercia es constante) y homogénea. Su ecuación característica es $ r^2+k^2=0$, cuyas raíces son $ r=\pm k\hspace{0.5mm}i$, siendo su solución general

$\displaystyle z=C_1$   sen$\displaystyle \hspace{0.15mm}\left(kx\right)+C_2 \cos\left(kx\right)$ (15.5)

Las constantes $ C_1$ y $ C_2$ se calculan a partir de las condiciones de contorno.

  $\displaystyle x=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} C_2=0\vspace{0.25cm}$ (15.6)
  $\displaystyle x=L \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} C_1$   sen$\displaystyle \hspace{0.15mm}\left(kL\right)=0$ (15.7)

La ecuación (15.7) tiene dos soluciones posibles: $ C_1=0$ ó sen$ \hspace{0.15mm}\left(kL\right)=0$. Si la primera solución es la correcta, se verifica que $ C_1=C_2=0$; es decir, los desplazamientos z son nulos y la barra queda en la configuración inicial. En el segundo caso $ k\hspace{0.5mm}L=n\pi$, siendo n un número entero, arbitrario, mayor que 1. Teniendo en cuenta la expresión de $ k^2$, se obtiene

$\displaystyle k^2=\displaystyle\frac{n^2\pi^2}{L^2}=\displaystyle\frac{P}{EI_y}... ...e{0.25cm} \Rightarrow \hspace{0.25cm} P=\displaystyle\frac{n^2\pi^2 EI_y}{L^2}$ (15.8)

La ecuación anterior implica que para que la barra mantenga la forma curvilínea es necesario que la fuerza P tenga unos valores determinados. La fuerza mínima, $ P_{\text{cr\'{\i}t}}$, no igual a cero, se obtiene cuando $ n = 1$.

$\displaystyle P_{\text{cr\'{\i}t}}=\displaystyle\frac{\pi^2EI_y}{L^2}$ (15.9)

Esta fuerza se denomina primera carga crítica o fuerza de Euler. Cuando $ n = 1$, $ k\hspace{0.5mm} L=\pi$ y la ecuación de la línea elástica (15.5) es

$\displaystyle z=C_1$   sen$\displaystyle \hspace{0.15mm}\left(\displaystyle\frac{\pi x}{L}\right)$ (15.10)

La barra se flexiona según una semionda sinusoidal cuya amplitud máxima es $ C_1$. Para cualquier otro valor entero de n, la ecuación de la línea elástica es

$\displaystyle z=C_1$   sen$\displaystyle \hspace{0.15mm}\left(\displaystyle\frac{n\pi x}{L}\right)$ (15.11)

Es decir, la línea elástica de la barra se representa por una curva compuesta por n semiondas, como muestra la Figura 15.5, que corresponden a las diferentes configuraciones de equilibrio de la misma.

Figura: 15.5 Posibles configuraciones de equilibrio de la barra de Euler
Image 05-Pandeo

La ecuación (15.11) depende del valor de la constante $ C_1$, por lo que se podría pensar en un equilibrio indiferente al ser posibles infinitas configuraciones de equilibrio correspondientes a los distintos valores de $ C_1$. Sin embargo, se ha admitido en el desarrollo realizado la hipótesis de pequeños desplazamientos, lo cual no es admisible cuando la carga es superior a $ P_{\text{cr\'{\i}t}}$, ya que las deformaciones aumentarán con gran rapidez (como se comprueba experimentalmente) y no se puede prescindir del término $ z'^2$. En dicho caso hay que utilizar la ecuación diferencial

$\displaystyle \displaystyle\frac{EI_yz''}{\left(1+z'^2\right)^\frac{3}{2}}=-P\hspace{0.5mm}z$ (15.12)

Integrando esta ecuación y sustituyendo x por $ \frac{L}{2}$ se obtiene la flecha $ w\left(\frac{L}{2}\right)$ en el punto central

$\displaystyle w\left(\frac{L}{2}\right)=\displaystyle\frac{L\sqrt{8}}{\pi}\sqrt... ...yle\frac{1}{8}\left(\displaystyle\frac{P}{P_{\text{cr\'{\i}t}}-1}\right)\right]$ (15.13)

Observando esta expresión se obtienen las siguientes conclusiones:

Como para cada valor de P corresponde una deformada diferente, no hay posiciones de equilibrio indiferente. Si crece P por encima de $ P_{\text{cr\'{\i}t}}$, la flecha aumenta muy rápidamente.

Figura: 15.6 Curvas carga-desplazamiento. Rama A: Pilar ideal elástico con pequeños desplazamientos. Rama B: Pilar ideal elástico con grandes desplazamientos
Image 06-Pandeo

La rama B de la gráfica de la Figura 15.6 se observa como al alcanzar el pilar la carga crítica, se requiere una carga creciente para producir un aumento del desplazamiento. En la misma figura se ha representado el desplazamiento considerando pequeños desplazamientos (rama A), donde se observa que el desplazamiento no está definido a partir de la carga crítica.