Cálculo de desplazamientos por métodos energéticos. Teorema de las Fuerzas Virtuales

Este teorema sólo se va a aplicar a barras esbeltas, con la directriz contenida en el plano XZ con las cargas actuando en dicho plano, y cuya sección transversal presenta simetría respecto al eje z.

El Teorema de las Fuerzas Virtuales (TFV) se enuncia de la siguiente forma: la condición necesaria y suficiente para que un campo de desplazamientos $ u_i$ sea compatible con un campo de deformaciones $ \varepsilon_{ij}$ es que se cumpla la igualdad de trabajos internos y externos, para todo campo de tensiones $ \sigma_{ij}^*$ en equilibrio con unas cargas exteriores $ X_i^*$ y $ t_i^*$

$\displaystyle \underbrace{\int_V \sigma_{ij}^* \varepsilon_{ij} dV}_{trabajo \t... ...V x_i^* u_i \text{d}V+\int_S t_i^{c*} u_i^c \text{d}S}_{\text{trabajo externo}}$ (13.22)

Considerando un estado de fuerzas y esfuerzos virtuales en equilibrio, el trabajo virtual complementario realizado por los esfuerzos virtuales al moverse sobre las deformaciones reales es

\begin{displaymath}\begin{array}{c} \int_V \left(\sigma^*\right)^T \varepsilon ... ...\frac{M_y^*(x)M_y(x)}{E(x)I_y(x)}z\right)\text{d}x \end{array}\end{displaymath} (13.23)

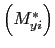Si sobre la barra se aplican fuerzas virtuales $ \left(F_{xi}^* ,F_{zi}^* \right)$ y/o momentos virtuales $ \left(M_{yi}^*\right)$ en n puntos, el trabajo virtual externo es

$\displaystyle \int_V x_i^* u_i$   d$\displaystyle V+\int_S t_i^{c*} u_i^c$   d$\displaystyle S=\sum_{i=1}^n \left(F_{xi}^* u_{xi}+F_{zi}^*w_{zi}+M_{yi}^*\theta_{yi}\right)$ (13.24)

siendo $ u_{xi}, w_{zi}$ los desplazamientos del punto i según los ejes x y z, y $ \theta_{yi}$ el giro del punto i alrededor del eje y. Así pues, la expresión del TFV para una barra esbelta es

\begin{displaymath}\begin{array}{c} \displaystyle\sum_{i=1}^n \left(F_{xi}^* u_... ...\frac{M_y^*(x)M_y(x)}{E(x)I_y(x)}z\right)\text{d}x \end{array}\end{displaymath} (13.25)

Si la estructura está formada por b barras esbeltas, con fuerzas $ \left(F_{xi} ,F_{zi} \right)$ y/o momentos $ \left(M_{yi}\right)$ en n puntos, la ecuación (13.25) es

\begin{displaymath}\begin{array}{c} \displaystyle\sum_{i=1}^n \left(F_{xi}^* u_... ...\frac{M_y^*(x)M_y(x)}{E(x)I_y(x)}z\right)\text{d}x \end{array}\end{displaymath} (13.26)

Si los valores de los esfuerzos y las propiedades de las barras son constantes ($ S_j = cte$, $ E_j = cte$, $ N_j = cte$, $ M_{yj}= cte$, e $ I_{yj} = cte$), la ecuación (13.26) queda en la forma

$\displaystyle \displaystyle\sum_{i=1}^n \left(F_{xi}^* u_{xi}+F_{zi}^*w_{zi}+M_... ...^b \left(\frac{N_j^*N_jL_j}{E_jA_j}+\frac{M_{yj}^*M_{yj}L_j}{E_jI_{yj}}\right)$ (13.27)

Para la aplicación de éste método, lo único que se requiere es que el sistema de cargas que actúa sobre la estructura esté en equilibrio. Puede tomarse como estructura virtual la real sin apoyos y sometida a un estado de cargas resultante de equilibrar la carga o momento unitario (aplicada en la sección cuyo desplazamiento o giro se desea calcular) con cargas y/o momentos aplicados en secciones cuyo desplazamiento y/o giro sea conocido en la estructura real y en la dirección de éstos.