 |
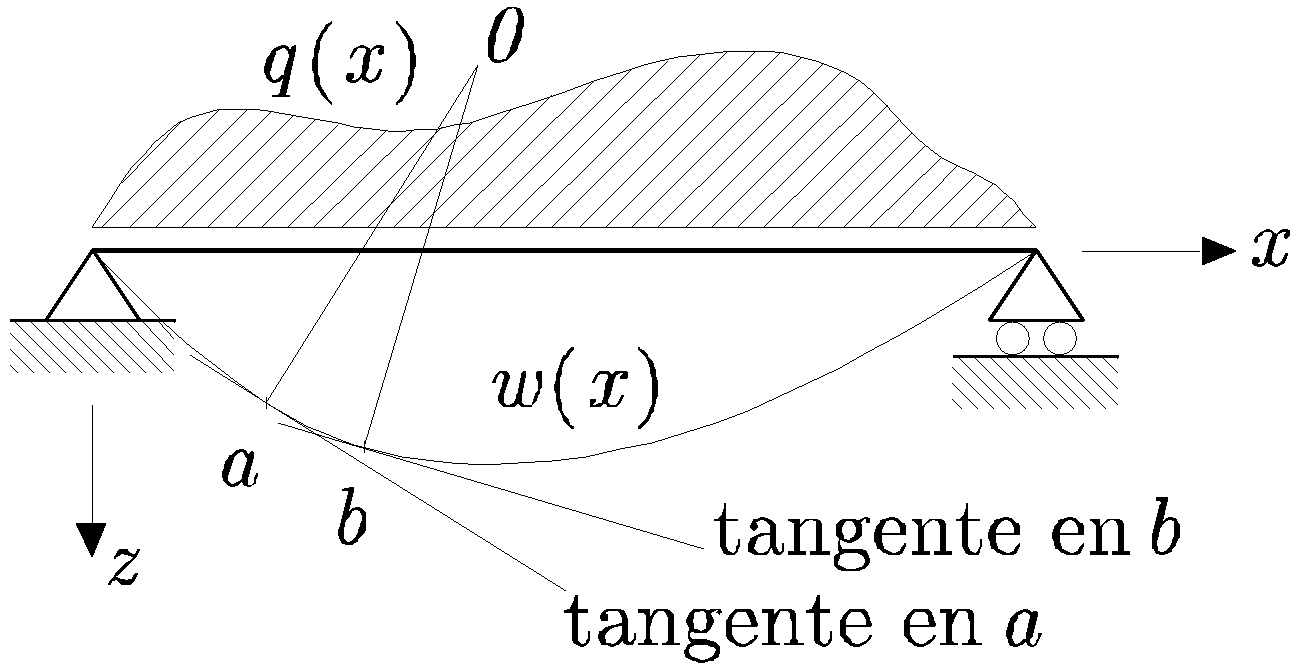
La curva (línea) elástica es la configuración que adopta la directriz de una barra prismática trabajando a flexión. El análisis que se desarrolla a continuación es válido para barras rectas que se deforman elásticamente por cargas contenidas en el plano de simetría de la sección transversal y aplicadas perpendicularmente al eje x de la barra. El eje x coincide con la directriz de la barra y su sentido positivo es hacia la derecha. El eje z se dispone con sentido positivo hacia abajo. La ecuación de la curva elástica se denotará por w y es función de x, como se muestra en la Figura 13.1.
Sean dos secciones muy próximas, a y b, separadas una distancia ds sobre la línea elástica, que se muestra el detalle ampliado en la Figura 13.2 para mayor claridad. El ángulo que la tangente en a forma con el eje x se denotará con ![]() . La tangente al punto b forma un ángulo
. La tangente al punto b forma un ángulo
![]() d
d![]() con el eje x. Por tanto, ambas tangentes forman un ángulo
d
con el eje x. Por tanto, ambas tangentes forman un ángulo
d![]() .
.
El arco ds puede expresarse en función del radio de curvatura ![]() y del ángulo entre las dos tangentes
d
y del ángulo entre las dos tangentes
d![]() como
como
siendo la curvatura
Considerando la hipótesis de pequeñas deformaciones, se puede admitir que
d![]() d
d![]() y
y
![]() , con lo que la ecuación (13.2) queda como
, con lo que la ecuación (13.2) queda como
siendo w el desplazamiento en dirección z.
Sustituyendo en (13.3) las expresiones obtenidas en el apartado 8.3
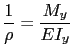 |
se obtiene
Para el sistema de ejes considerado, cuando la curva elástica es cóncava hacia arriba (convexa), la pendiente
![]() es algebraicamente decreciente con x, como se muestra en la Figura 13.3 a), por tanto,
es algebraicamente decreciente con x, como se muestra en la Figura 13.3 a), por tanto,
![]() es negativa. Del mismo modo, cuando la curva es cóncava hacia abajo, la pendiente
es negativa. Del mismo modo, cuando la curva es cóncava hacia abajo, la pendiente
![]() es algebraicamente creciente con x, como se muestra en la Figura 13.3 b), por tanto,
es algebraicamente creciente con x, como se muestra en la Figura 13.3 b), por tanto,
![]() es positiva.
es positiva.
Según el criterio de signos adoptado para los esfuerzos en el tema 6, los momentos flectores son positivos cuando producen tracciones en las fibras inferiores de la barra, referida ésta a un sistema de ejes local como el mostrado en la Figura 13.3. Por lo tanto, los momentos positivos disminuyen en el sentido algebraico la curvatura, mientras que los momentos negativos la aumentan. Por consiguiente, la ecuación (13.4), para poder ser aplicada de acuerdo con los criterios considerados debe escribirse como
La ecuación anterior es válida siempre que todos los puntos de la barra presenten un comportamiento elástico y las deformaciones sean pequeñas. Debe tenerse presente también que en la obtención de dicha ecuación no se han considerado las deformaciones debidas al esfuerzo cortante.
Integrando una vez (13.5) se obtiene la ecuación de la pendiente de la curva elástica, e integrando dos veces, se obtiene la curva elástica. En la integración de (13.5) aparecen 2n constantes de integración, siendo n el número de tramos necesarios para la obtención de la ley de flectores. Para determinar estas constantes de integración es necesario considerar las condiciones de contorno de la barra. Si con éstas no fuera suficiente, se impondrán condiciones de compatibilidad de desplazamientos y giros en los puntos comunes entre tramos considerados en la barra para el cálculo de la ley de momentos.
La ecuación (13.5) puede escribirse de forma alternativa, derivando una vez cada miembro de la ecuación respecto de x
Derivando de nuevo respecto de x, se obtiene
(13.6) y (13.7) son las ecuaciones diferenciales de la curva elástica en función del cortante y de la carga aplicada, respectivamente.
Si se prescinde de la hipótesis de pequeñas deformaciones, no es admisible aproximar la tangente al ángulo, por tanto
Por otro lado, el arco ds puede expresarse en función de dx y dw, como
Habiéndose obtenido la última relación de (13.9) dividiendo ds por dx. Derivando (13.8) se obtiene
Sustituyendo (13.9) y (13.10) en (13.2), se obtiene
Finalmente, sustituyendo (13.11) en (13.4), la ecuación diferencial de la curva elástica para grandes deformaciones es