 |
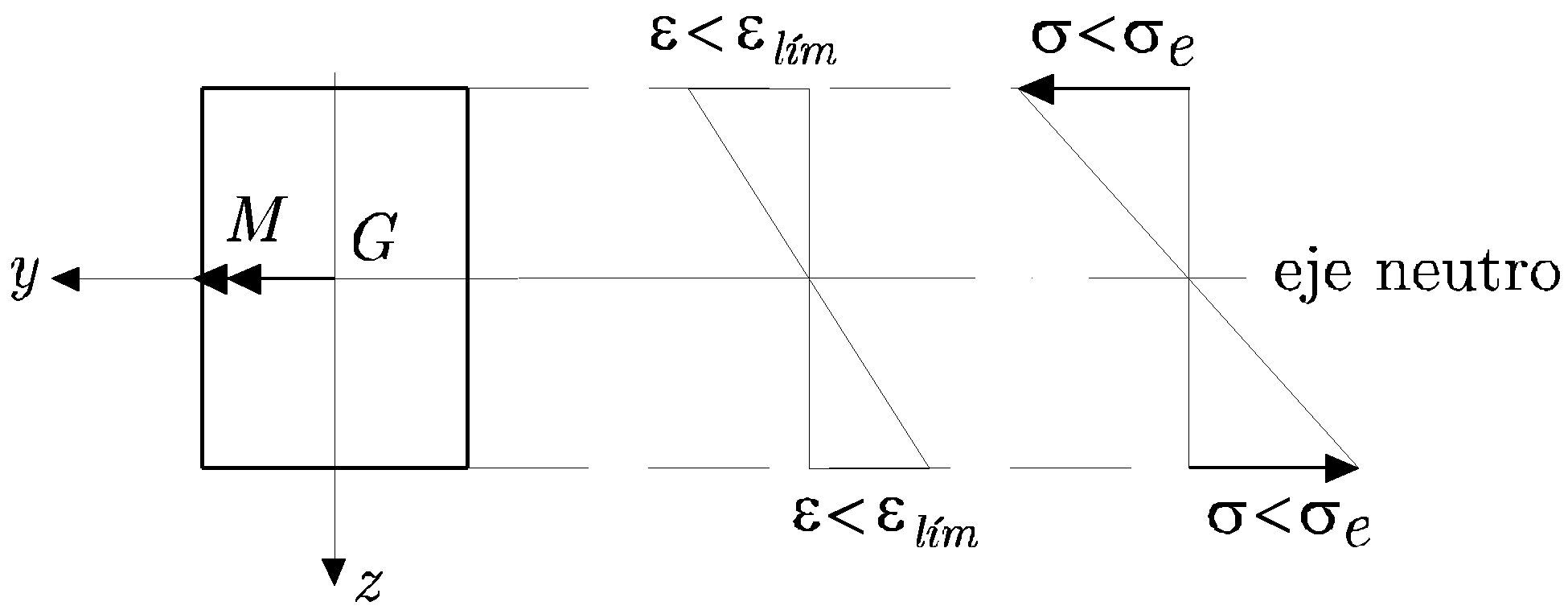
En la Figura 12.2 se muestran una sección bisimétrica sometida a un momento flector según el eje y, y los diagramas planos de las distribuciones de deformaciones longitudinales y tensiones normales correspondientes. En ninguna de la fibras se ha alcanzado la deformación del límite elástico y en consecuencia las tensiones en cualquier punto de la sección están por debajo del límite elástico del material.
Las distribuciones de tensiones y deformaciones son lineales, respondiendo a las ecuaciones
siendo E el módulo de elasticidad longitudinal y ![]() la curvatura de la sección. Considerando una rebanada diferencial de un elemento estructural, la curvatura
la curvatura de la sección. Considerando una rebanada diferencial de un elemento estructural, la curvatura ![]() de la sección es el ángulo que se inclina una cara de la rebanada respecto de la otra, dividido por la distancia que las separa. Si se consideran dos secciones separadas una unidad de longitud, la curvatura es
de la sección es el ángulo que se inclina una cara de la rebanada respecto de la otra, dividido por la distancia que las separa. Si se consideran dos secciones separadas una unidad de longitud, la curvatura es
Si el momento flector se va incrementando, la tensión y la deformación en cada fibra de la sección aumentan. Habrá un valor de ![]() para el que la deformación en las fibra extremas (las más tensionadas) coincida con la deformación en el límite elástico,
para el que la deformación en las fibra extremas (las más tensionadas) coincida con la deformación en el límite elástico,
![]() , correspondiéndoles la tensión del límite elástico,
, correspondiéndoles la tensión del límite elástico, ![]() . En la Figura 12.3 se muestran los diagramas planos de las distribuciones de deformaciones longitudinales y tensiones normales.
. En la Figura 12.3 se muestran los diagramas planos de las distribuciones de deformaciones longitudinales y tensiones normales.
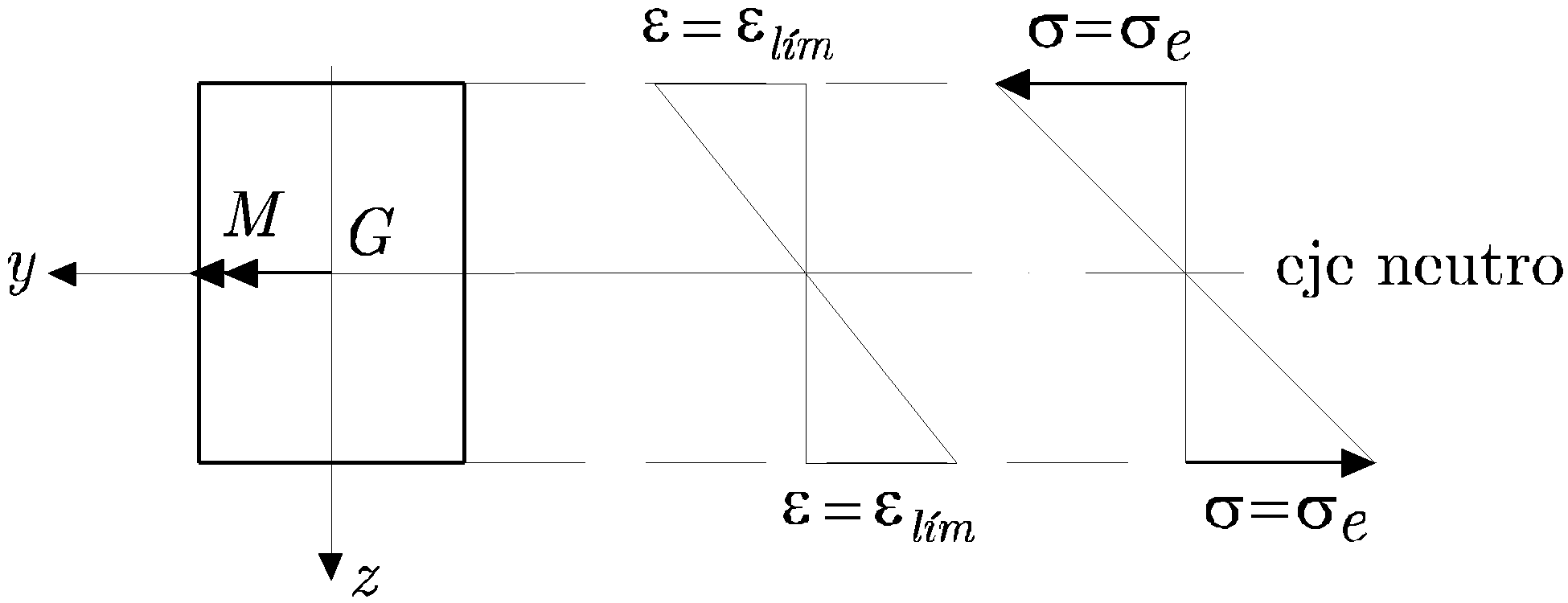 |
Si se sigue incrementando el momento flector, se llegará a un estado tal que las fibras extremas de la sección habrán superado la deformación correspondiente al límite elástico junto con parte de las contiguas, trabajando todas ellas a una misma tensión ![]() . En la Figura 12.4 se muestran los diagramas planos de las distribuciones de deformaciones longitudinales y tensiones normales correspondientes.
. En la Figura 12.4 se muestran los diagramas planos de las distribuciones de deformaciones longitudinales y tensiones normales correspondientes.
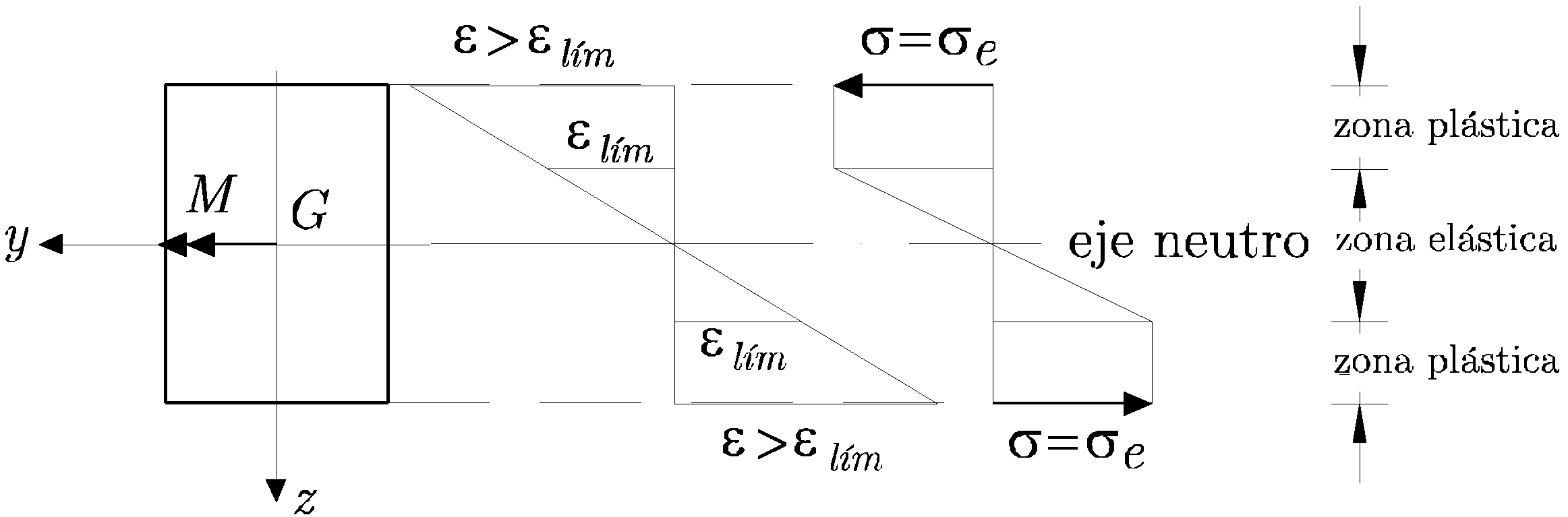
Si se sigue incrementando ![]() , habrá una extensa zona de la sección donde todas las fibras superen la deformación correspondiente al límite elástico y por tanto trabajen a la tensión del límite elástico, como se muestra en la Figura 12.5.
, habrá una extensa zona de la sección donde todas las fibras superen la deformación correspondiente al límite elástico y por tanto trabajen a la tensión del límite elástico, como se muestra en la Figura 12.5.
 |
La deformación en el límite elástico para un acero es función del tipo de acero, estando acotada entre
![]() para un acero con
para un acero con
![]() MPa y
MPa y
![]() para un acero con
para un acero con
![]() MPa.
MPa.
Considerando una deformación longitudinal unitaria en rotura para el acero de
![]() , cuando en la fibra más tensionada de la sección se alcance la deformación correspondiente a la rotura, la zona de la sección trabajando en régimen elástico, que se muestra en la Figura 12.6, será
, cuando en la fibra más tensionada de la sección se alcance la deformación correspondiente a la rotura, la zona de la sección trabajando en régimen elástico, que se muestra en la Figura 12.6, será
es decir, la zona elástica tiene una extensión como máximo el doble de ![]() (en el caso de que la sea sección simétrica respecto al eje neutro), siendo
(en el caso de que la sea sección simétrica respecto al eje neutro), siendo ![]()
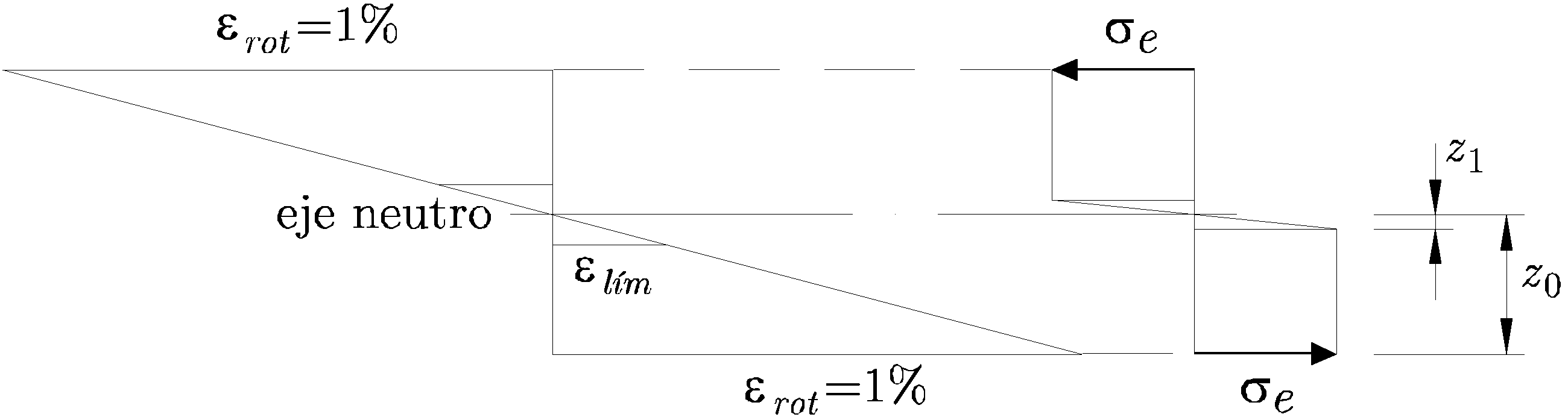 |
Así, para un acero con
![]() , la zona trabajando en régimen elástico será, como máximo,
, la zona trabajando en régimen elástico será, como máximo,
De la ecuación (12.6) se deduce que dicha zona es muy pequeña en relación con la zona plastificada. Por este motivo se acepta la distribución de tensiones mostrada en la Figura 12.7, en la que toda la sección está totalmente plastificada. Dicha distribución corresponde al caso, teórico, de curvatura infinita de la sección.
El momento que produce el estado tensional mostrado en la Figura 12.7 recibe el nombre de momento plástico, ![]() . Al ser dicho momento estáticamente equivalente al momento producido por la distribución de tensiones normales, ha de cumplirse que
. Al ser dicho momento estáticamente equivalente al momento producido por la distribución de tensiones normales, ha de cumplirse que
siendo ![]() y
y ![]() las alturas, en valor absoluto, de las zonas traccionada y comprimida, respectivamente y b el ancho de la sección. Al ser
las alturas, en valor absoluto, de las zonas traccionada y comprimida, respectivamente y b el ancho de la sección. Al ser
![]() en la zona traccionada y
en la zona traccionada y
![]() en la zona comprimida, sustituyendo en (12.7) se obtiene
en la zona comprimida, sustituyendo en (12.7) se obtiene
Las integrales corresponden a los momentos estáticos de las áreas traccionada y comprimida de la sección respecto al eje neutro. Por tanto, (12.8) se puede reescribir (considerando los valores absolutos de ![]() y
y ![]() ) como
) como
La tensión en un punto en función del módulo resistente asociado a dicho punto se puede expresar como
siendo h la mínima distancia del punto al eje neutro. El momento elástico ![]() , a partir de la ecuación (12.10), puede expresarse como
, a partir de la ecuación (12.10), puede expresarse como
Comparando las ecuaciones (12.9) y (12.11), el momento plástico puede ser expresado en la forma
siendo ![]() el módulo plástico de la sección
el módulo plástico de la sección
La relación entre los momentos plástico (![]() ) y elástico (
) y elástico (![]() ) da una idea de la mayor resistencia de la sección cuando trabaja en régimen plástico.
) da una idea de la mayor resistencia de la sección cuando trabaja en régimen plástico.
Esta relación se denomina factor de forma y se denota con la letra griega ![]() . El factor de forma depende exclusivamente de la geometría de la sección (tanto
. El factor de forma depende exclusivamente de la geometría de la sección (tanto ![]() como
como ![]() son solamente función de la geometría de la sección). Cuanto menor sea el factor de forma de una sección, mejor estará diseñada para trabajar a flexión.
son solamente función de la geometría de la sección). Cuanto menor sea el factor de forma de una sección, mejor estará diseñada para trabajar a flexión.
Para determinar la posición del eje neutro en una sección plastificada se van a plantear los equilibrios de fuerzas y de momentos de la sección.
Sea una sección sometida a un sistema de cargas contenidas en un mismo plano, tal que producen un momento flector que plastifica la sección.
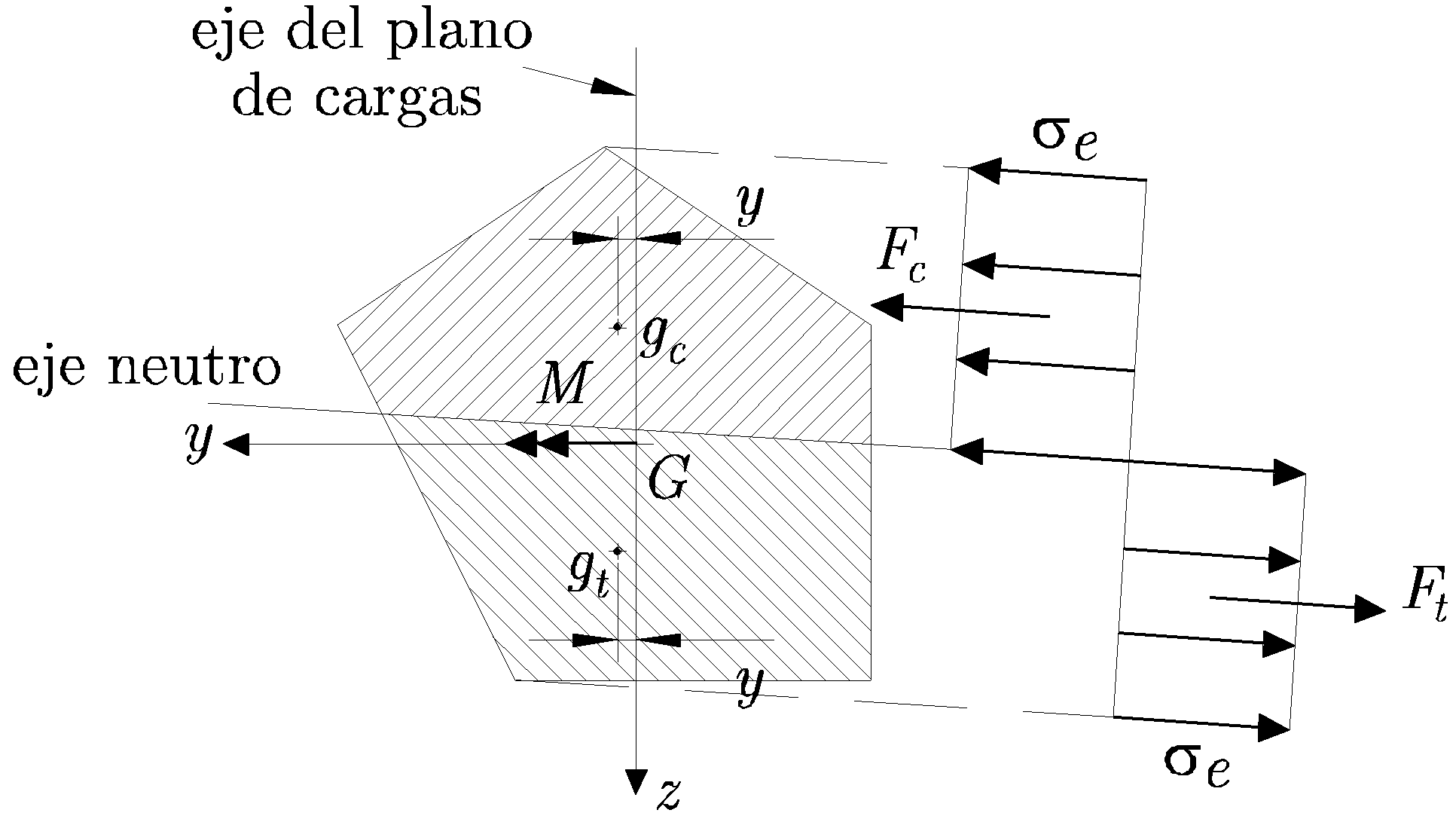 |
En la Figura 12.8 se muestra la distribución de tensiones correspondientes y la posición del eje neutro. Planteando el equilibrio de fuerzas (las resultantes de la distribución de tensiones propuesta), se ha de verificar
es decir,
siendo ![]() ,
, ![]() ,
, ![]() y
y ![]() las resultantes y las áreas de las zonas comprimida y traccionada, respectivamente. De (12.16) se deduce que las áreas de las zonas comprimida y traccionada son iguales en una sección totalmente plastificada sometida a flexión pura y, obviamente, dichas áreas coinciden con la mitad del área S de la sección.
las resultantes y las áreas de las zonas comprimida y traccionada, respectivamente. De (12.16) se deduce que las áreas de las zonas comprimida y traccionada son iguales en una sección totalmente plastificada sometida a flexión pura y, obviamente, dichas áreas coinciden con la mitad del área S de la sección.
La conclusión expresada en (12.17) implica que el eje neutro, en secciones asimétricas totalmente plastificadas, no pasa por el centro de gravedad de la sección.
Planteando el equilibrio de momentos respecto al eje que resulta de la intersección del plano de cargas con la sección, eje del plano de cargas, se obtiene
Al ser las áreas comprimida y traccionada iguales
siendo las integrales los momentos estáticos de las zonas traccionada y comprimida respecto al eje del plano de cargas con la sección. Por tanto, se concluye que el eje neutro en una sección totalmente plastificada divide a la sección en dos zonas cuyos momentos estáticos respecto al eje del plano de cargas son iguales.
Al ser iguales las áreas traccionada y comprimida, los centros de gravedad de ambas zonas se encuentran sobre una misma recta que además es paralela al eje del plano de cargas, como muestra la Figura 12.8. Por consiguiente, si el eje del plano de cargas es de simetría, el eje neutro de la sección totalmente plastificada será perpendicular al eje del plano de cargas.
En la Figura 12.9 se muestra la misma sección, divida en dos áreas iguales pero diferentes a las realizadas en (12.8). Se comprueba que los centros de gravedad de estas áreas no coinciden sobre una misma línea, paralela al eje del plano de cargas, por lo que no se verifica la ecuación (12.19) y el eje neutro mostrado no es posible.
El diagrama momento-curvatura de una sección describe el comportamiento resistente de la misma.
Al actuar un momento sobre una rebanada diferencial, ésta se curva manteniéndose las caras de la misma planas y por tanto, existiendo una distribución también plana de deformaciones. Al ir aumentando el momento, se va incrementando la curvatura de la sección. El diagrama momento-curvatura se obtiene representando en un diagrama de abscisa la curvatura y de ordenada el momento, para distintos valores del momento la curvatura obtenida. Dicho diagrama tiene una parte lineal, de ecuación
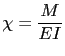 . Sigue una parte no lineal, y finalmente el diagrama acaba en
. Sigue una parte no lineal, y finalmente el diagrama acaba en ![]() con una curvatura infinita (rama asintótica de la gráfica de la Figura 12.10). La curvatura en la parte no lineal se puede obtener mediante la expresión
con una curvatura infinita (rama asintótica de la gráfica de la Figura 12.10). La curvatura en la parte no lineal se puede obtener mediante la expresión
![]() . Siendo
. Siendo ![]() la profundidad de la zona elástica comprimida.
la profundidad de la zona elástica comprimida.