Secciones abiertas

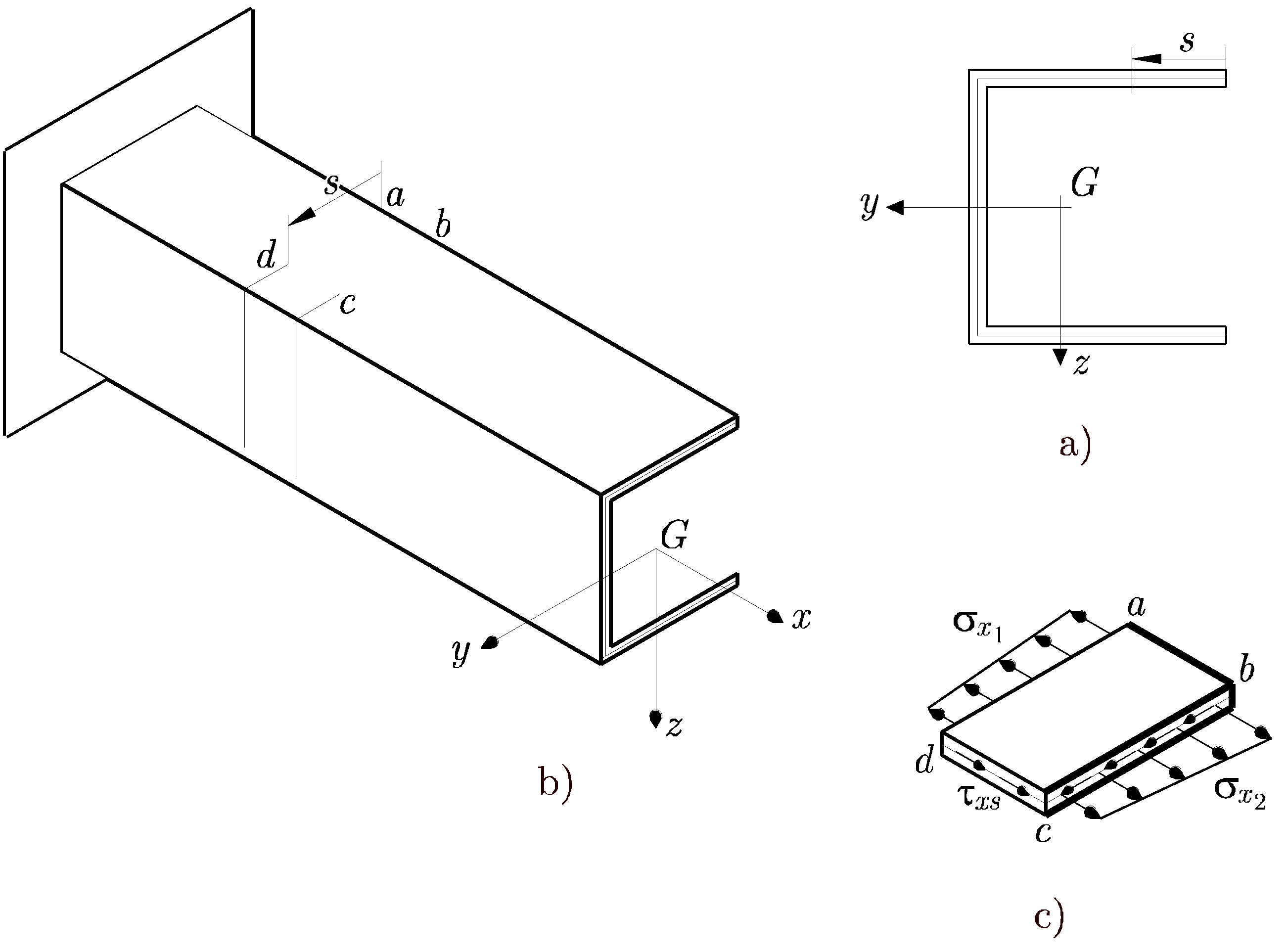
Sea una barra con sección transversal arbitraria, como la que se muestra en la Figura 9.8 a), que cumple las condiciones de pared delgada. Los ejes y y z son principales de inercia.

Figura 9.8: Barra prismática de sección transversal abierta de pared delgada
Image 08-FSimple

Se supondrá que el sistema de cargas es tal que provoca únicamente flexión en el plano $ XZ$, siendo el eje y el eje neutro. La tensión normal en cualquier punto de la barra será

$\displaystyle \sigma_x\left(x,s\right)=\displaystyle\frac{M_y\left(x\right)}{I_y}z$ (9.15)

siendo s una coordenada curvilínea que se mide sobre la línea media del perfil (línea de trazos fina) a partir del origen escogido.

Se estudiará un elemento de volumen diferencial, abcd, con uno de sus lados, el ab, coincidente con el borde de la sección. El otro lado tiene longitud s, medida a lo largo de la línea media de la sección, como se muestra en la Figura 9.8 b). Al igual que ocurría en las secciones macizas, la variación del momento flector a un lado y otro del volumen considerado implica tensiones diferentes a ambos lados, como se puede ver en la Figura 9.8 c) por lo que son necesarias las tensiones tangenciales para conseguir el equilibrio. El equilibrio del volumen diferencial considerado implica que

$\displaystyle \tau_{xs}\left(x,s\right) \hspace{1mm} t\left(s\right)$   d$\displaystyle x+\int^s_0 \sigma_{x2}$   d$\displaystyle S-\int^s_0 \sigma_{x1}$   d$\displaystyle S=0$ (9.16)

siendo $ t\left(s\right)$ el espesor del volumen diferencial (que puede variar con s). Sustituyendo (9.15) en (9.16), se obtiene

$\displaystyle \tau_{xs}\left(x,s\right) \hspace{1mm} t\left(s\right)$   d$\displaystyle x+\displaystyle\frac{M_{y2}\left(x\right)}{I_y} \int^s_0 z$   d$\displaystyle S-\displaystyle\frac{M_{y1}\left(x\right)}{I_y} \int^s_0 z$   d$\displaystyle S$ (9.17)

y despejando la tensión tangencial se llega a la expresión

$\displaystyle \tau_{xs}\left(x,s\right)=-\displaystyle\frac{\text{d}M_y\left(x\... ...frac{V_z\left(x\right)}{I_y \hspace{1mm} t(s)}\int^s_0 z \hspace{1mm} \text{d}S$ (9.18)

donde se ha tenido en cuenta que la variación del momento flector respecto a x, es el esfuerzo cortante. La integral que aparece en (9.18) es el momento estático del trozo de sección transversal de longitud s, respecto al eje y. La ecuación (9.18) adopta una forma similar a la (9.6) obtenida para el caso de secciones macizas

$\displaystyle \tau_{xs}\left(x,s\right)=-\displaystyle\frac{V_z\left(x\right) Q_y\left(s\right)}{I_y \hspace{1mm} t\left(s\right)}$ (9.19)

A diferencia de la distribución de tensiones en perfiles de sección maciza, en perfiles de pared delgada la tensión tangencial se supone constante en el espesor. Las tensiones tangenciales están dirigidas a lo largo de la línea media de la sección transversal y actúan paralelas a los bordes de la sección. Se define el flujo de tensiones en cualquier punto de la sección transversal como

$\displaystyle q_{xs}\left(x,s\right)=\tau_{xs}\left(x,s\right) \hspace{1mm} t\left(s\right)=-\displaystyle\frac{V_z\left(x\right) Q_y\left(s\right)}{I_y}$ (9.20)

Al ser $ V_z$ e $ I_y$ constantes, el flujo de tensiones es directamente proporcional a $ Q_y\left(s\right)$. En los extremos de las alas de la sección, $ Q_y\left(s\right)$ es cero, por lo que el flujo de tensiones también es cero. El valor máximo del flujo de tensiones, que varía de forma continua de un extremo a otro de la sección, se obtiene en el eje neutro, donde $ Q_y\left(s\right)$ es máximo.

Si existen simultáneamente cortantes en las direcciones de los ejes y y z, la expresión 9.20 se transforma en

$\displaystyle \tau_{xs}\left(x,s\right)t\left(s\right)=-\displaystyle\frac{V_y\... ...t)}-\displaystyle\frac{V_z\left(x\right) Q_y\left(s\right)}{I_yt\left(s\right)}$ (9.21)

Si los ejes no son principales de inercia, la distribución de tensiones tangenciales es

\begin{displaymath}\begin{array}{c} \tau_{xs}\left(x,s\right) = \vspace{3mm} \\... ...) I_{yz}}{I_yI_z-I^2_{yz}}Q_y\left(s\right)\right) \end{array}\end{displaymath} (9.22)

siendo el flujo de tensiones

\begin{displaymath}\begin{array}{c} q_{xs}\left(x,s\right) = \vspace{3mm} \\ ... ...x\right) I_{yz}}{I_yI_z-I^2_{yz}}Q_y\left(s\right) \end{array}\end{displaymath} (9.23)