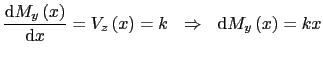Distribución de tensiones tangenciales estáticamente equivalentes a esfuerzos cortantes en barras de sección maciza

Si en una rebanada diferencial de una barra prismática, como la de la Figura 9.2, existe un esfuerzo cortante, constante en ambas caras, es porque existe una variación lineal del momento flector entre éstas:

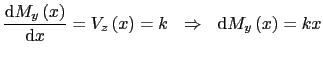$\displaystyle \displaystyle\frac{\text{d}M_y\left(x\right)}{\text{d}x}=V_z\left... ...ght)=k \hspace{0.25cm} \Rightarrow \hspace{0.25cm} \text{d}M_y\left(x\right)=kx$

**Figura 9.2:** Rebanada diferencial de un tramo de viga sometido a flexión simple

En el desarrollo que sigue se considerarán secciones simétricas respecto del eje z, con las cargas actuando en el plano de simetría XZ. El eje y pasa por el centro de gravedad de la sección y, junto con el z, son los ejes principales de inercia.

La distribución de tensiones normales en ambas caras de la rebanada se muestra en la Figura 9.3 a). La rebanada ha de estar en equilibrio, y cualquier trozo de ella, también. Sea un trozo de rebanada con su cara inferior a una altura z sobre el eje neutro, con ancho

a dicha altura y área S', tal como se muestra en la Figura 9.3 b).

**Figura 9.3:** Distribución de tensiones normales a ambos lados de una rebanada diferencial de un tramo de viga sometida a flexión simple

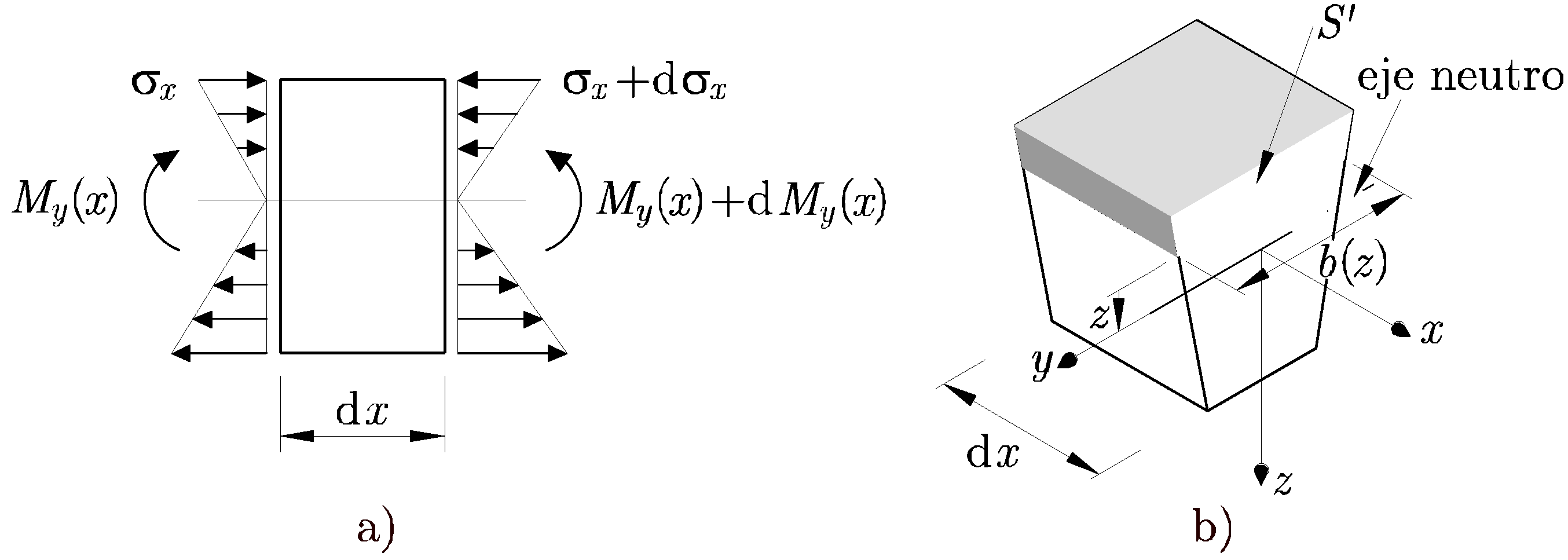Estableciendo el equilibrio de fuerzas en el trozo de rebanada diferencial, como se muestra en la Figura 9.4

**Figura 9.4:** Equilibrio de un trozo de la rebanada diferencial de un tramo de viga sometida a flexión simple

$\displaystyle \int_{S'}\sigma_{x1}\left(x,y,z\right)$ d $\displaystyle S+\tau_{zx}\left(x,y,z\right)\hspace{1mm} b(z)$ d $\displaystyle x - \int_{S'}\sigma_{x2}\left(x,y,z\right)$ d $\displaystyle S=0$

(9.1)

Las tensiones normales están producidas sólo por el momento flector, por lo que se pueden sustituir por la expresión (8.4), obteniéndose

$\displaystyle \int_{S'}\displaystyle\frac{M_y\left(x\right)}{I_y}z$ d $\displaystyle S+\tau_{zx}\left(x,y,z\right)\hspace{1mm} b(z)$ d $\displaystyle x - \int_{S'}\displaystyle\frac{M_y\left(x\right)+\text{d}M_y\left(x\right)}{I_y}z \hspace{1mm} \text{d}S=0$

(9.2)

$\displaystyle \displaystyle\frac{\text{d}M_y\left(x\right)}{I_y}\int_{S'}z \hsp... ...text{d}S-\tau_{zx}\left(x,y,z\right) \hspace{1mm} b(z) \hspace{1mm} \text{d}x=0$

(9.3)

$\displaystyle \tau_{zx}\left(x,y,z\right)=\displaystyle\frac{1}{b(z)I_y}\displaystyle\frac{\text{d}M_y\left(x\right)}{\text{d}x}\int_{S'}z \hspace{1mm} \text{d}S$

(9.4)

La integral representa el momento estático del área S' respecto al eje y, que se denotará por

. Teniendo en cuenta que la derivada del momento flector respecto a x es el esfuerzo cortante, (9.4) toma la forma

$\displaystyle \tau_{zx}\left(x,y,z\right)=\displaystyle\frac{Q_y(z)V_z\left(x\right)}{b(z)I_y}$

(9.5)

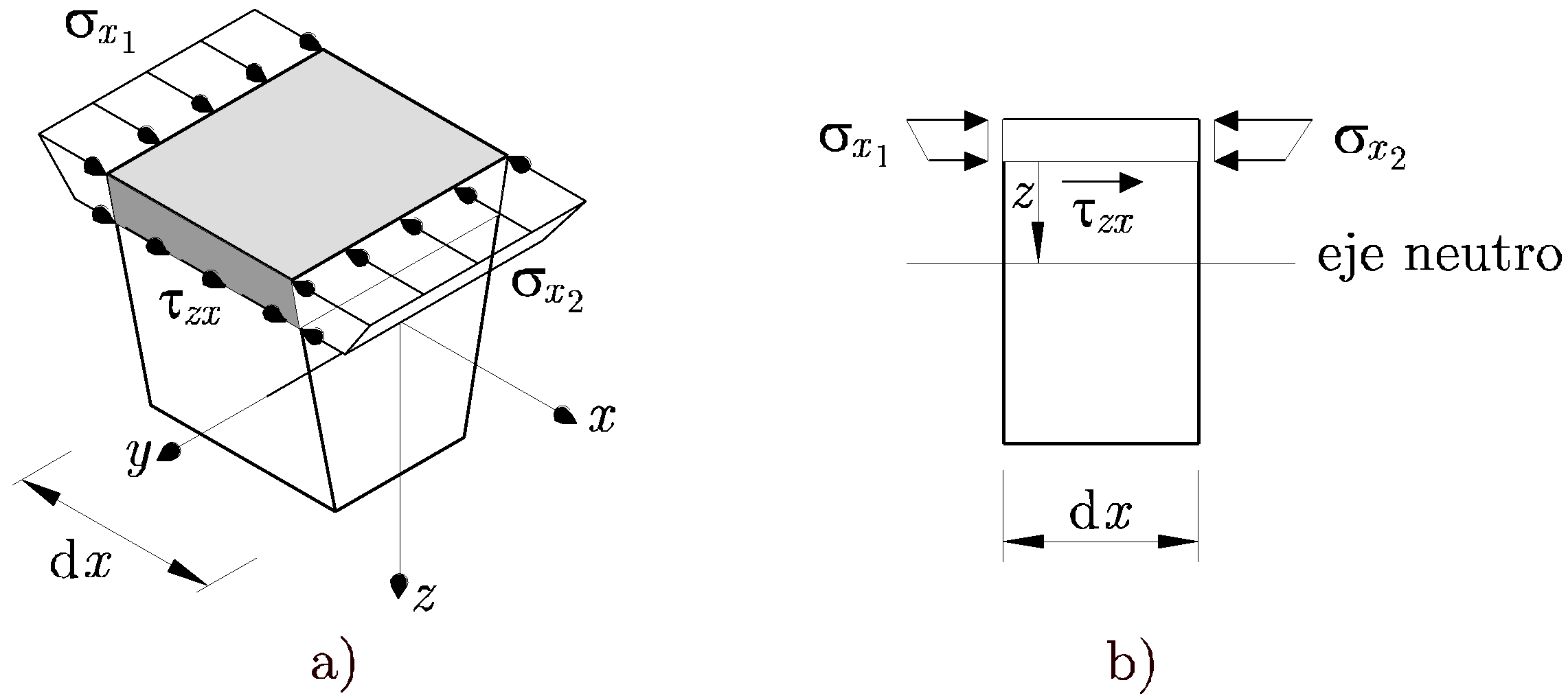
A la vista de la Figura 9.4 a) y de la Figura 9.4 b), las tensiones calculadas son las contenidas en el plano de separación de los trozos de la rebanada diferencial, es decir, las tensiones rasantes. De acuerdo con el principio de reciprocidad de las tensiones tangenciales, las tensiones tangenciales en las caras de la rebanada diferencial con normal el eje x, son las mismas, como se muestra en la Figura 9.5.

**Figura 9.5:** Tensiones tangenciales en las caras de la rebanada diferencial

$\displaystyle \tau_{xz}\left(x,y,z\right)=\displaystyle\frac{Q_y(z)V_z\left(x\right)}{b(z)I_y}$

(9.6)

Las secciones transversales de las barras sometidas a un esfuerzo cortante no se mantienen planas tras la deformación. Al ser en general variable la distribución de tensiones tangenciales sobre la sección, también varia la deformación angular. Esto se traduce en un alabeo de la sección transversal, como se muestra en la Figura 9.6.

Este alabeo no afecta de forma importante a las deformaciones longitudinales, por lo que para el cálculo de las tensiones debidas a flexión simple se utilizan las expresiones deducidas en los apartados anteriores.

En general, si los ejes de la sección no son principales de inercia y existen esfuerzos cortantes en las direcciones de los ejes y y z simultáneamente, se puede demostrar que las expresiones de las distribuciones de tensiones tangenciales son

$\begin{displaymath}\begin{array}{c} \tau_{xy}\left(x,y,z\right) = \vspace{3mm} ... ...)I_{yz}}{I_yI_z-I^2_{yz}}V_z\left(x\right) \right) \end{array}\end{displaymath}$

(9.7)

$\begin{displaymath}\begin{array}{c} \tau_{xz}\left(x,y,z\right) = \vspace{3mm} ... ...t)I_{yz}}{I_yI_z-I^2_{yz}}V_z\left(x\right)\right) \end{array}\end{displaymath}$

(9.8)

Si los ejes son principales de inercia, las expresiones anteriores se simplifican:

$\displaystyle \tau_{xy}\left(x,y,z\right)=\displaystyle\frac{1}{b(y)}\left(\dis... ...t(x\right) + \displaystyle\frac{Q_y\left(y\right)}{I_y}V_z\left(x\right)\right)$			(9.9)
$\displaystyle \tau_{xz}\left(x,y,z\right)=\displaystyle\frac{1}{b(z)}\left(\dis... ...t(x\right) + \displaystyle\frac{Q_y\left(z\right)}{I_y}V_z\left(x\right)\right)$			(9.10)

Las expresiones de los momentos estáticos $Q_y\left (y\right )$ , $Q_y\left (z\right )$ , $Q_z\left (y\right )$ y $Q_z\left (z\right )$ , que aparecen en las ecuaciones anteriores son

$\displaystyle Q_y\left(y\right)=S \hspace{1mm} z_g$			(9.11)
$\displaystyle Q_y\left(z\right)=S \hspace{1mm} z_g$			(9.12)
$\displaystyle Q_z\left(y\right)=S \hspace{1mm} y_g$			(9.13)
$\displaystyle Q_z\left(y\right)=S \hspace{1mm} y_g$			(9.14)

El subíndice en la denominación del momento estático indica el eje respecto al cual se calcula. Entre paréntesis se señala la coordenada con la que varía el área del elemento cuyo momento estático se desea calcular.

Si la sección presenta simetría respecto del eje y, se verifica que $Q_y\left(y\right)=0$ . Igualmente, si la sección presenta simetría respecto del eje z, se verifica que $Q_z\left(z\right)=0$ . Obviamente, si la sección presenta doble simetría, ambos serán nulos.

En la Figura 9.7 se muestra gráficamente el significado de estos momentos estáticos.

**Figura 9.7:** a) $Q_y\left (y\right )$ . b) $Q_y\left (z\right )$ . c) $Q_z\left (z\right )$ . d) $Q_z\left (y\right )$