 |
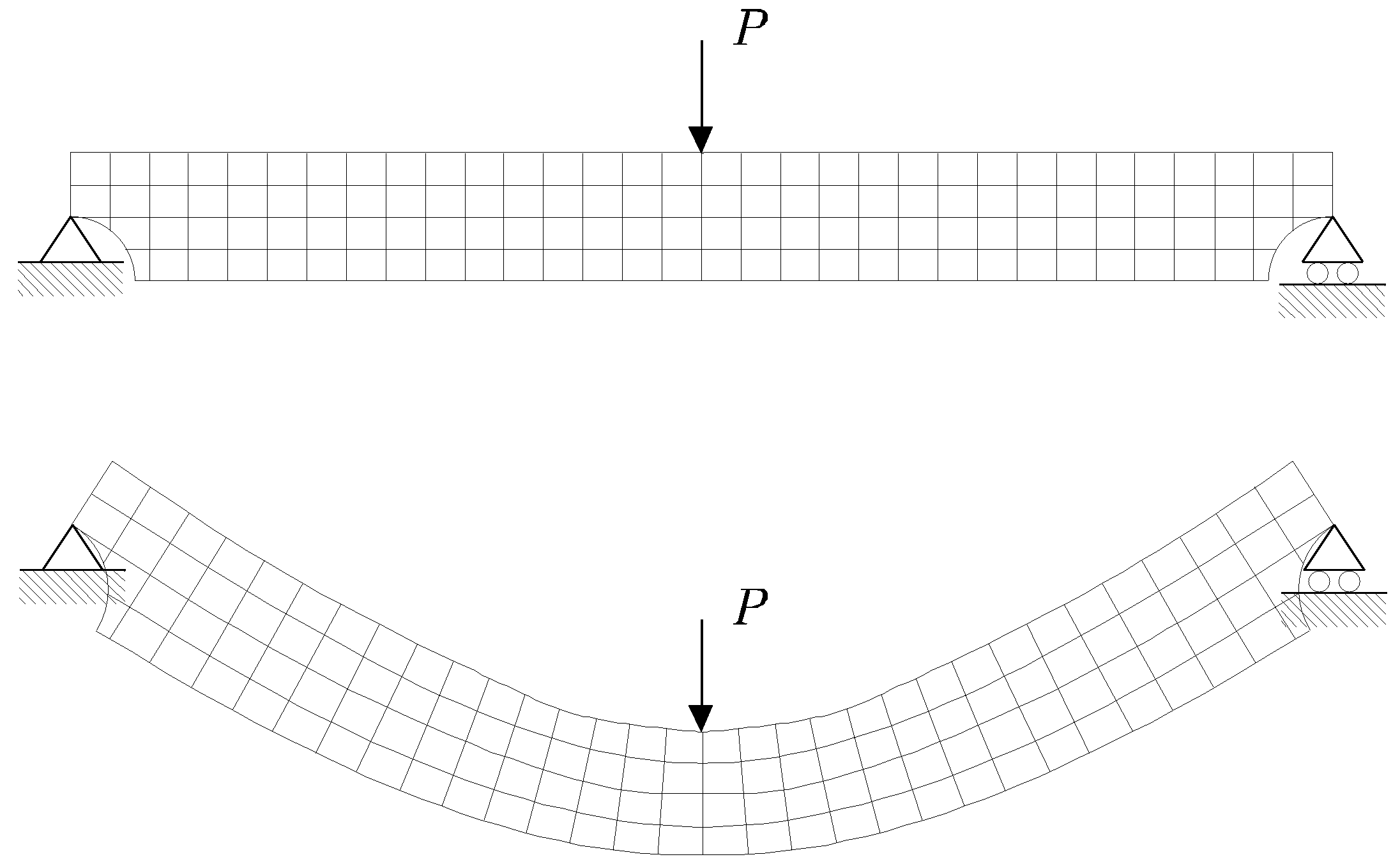
En la Figura 2.3 se muestra una viga biapoyada sometida a una carga puntual en su zona central, así como la configuración deformada de la misma.
Se aprecia la distorsión que sufre la malla superpuesta sobre la viga una vez deformada. Los cuadriláteros que forman la malla sufren un alargamiento o acortamiento de los lados que los forman y una variación de los ángulos rectos iniciales. Es decir, la posición relativa entre los puntos del sólido ha variado, por lo que la viga se ha deformado.
Para determinar la deformación producida se va a trabajar con dos puntos cualesquiera ![]() y
y ![]() de la viga, muy próximos, unidos por el vector de posición
de la viga, muy próximos, unidos por el vector de posición
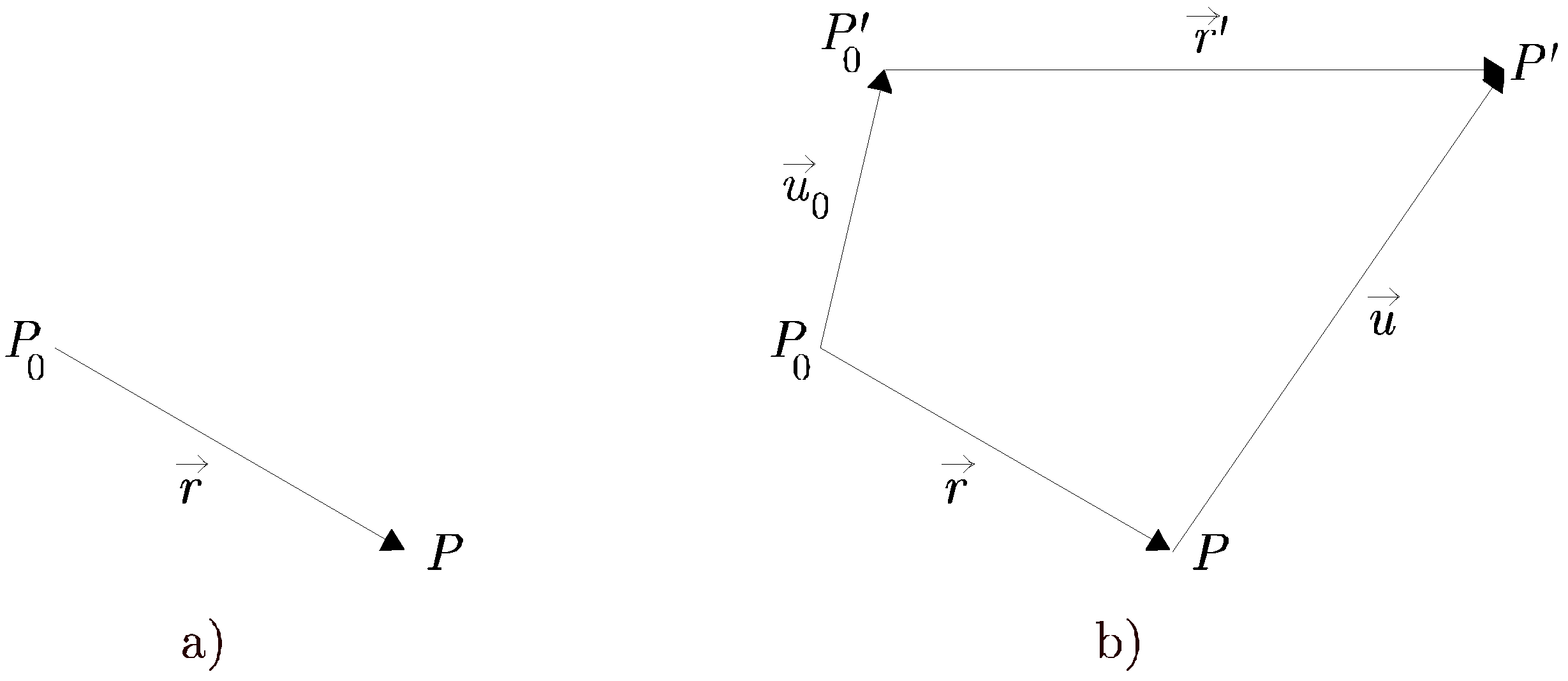
![]() que se muestra en la Figura 2.4 a). Al deformarse la viga, los puntos pasan, en la configuración deformada, a las posiciones
que se muestra en la Figura 2.4 a). Al deformarse la viga, los puntos pasan, en la configuración deformada, a las posiciones ![]() y
y ![]() que se muestran en la Figura 2.4 b). Considerando la hipótesis de pequeños desplazamientos se admite que las configuraciones deformada e indeformada prácticamente coinciden.
que se muestran en la Figura 2.4 b). Considerando la hipótesis de pequeños desplazamientos se admite que las configuraciones deformada e indeformada prácticamente coinciden.
 |
Denominamos vectores desplazamiento de los puntos ![]() y
y ![]() a
a
![]() y
y
![]() , respectivamente. Al estar muy próximos ambos puntos, es posible obtener el valor de
, respectivamente. Al estar muy próximos ambos puntos, es posible obtener el valor de
![]() utilizando el desarrollo en serie de Taylor en el entorno del punto
utilizando el desarrollo en serie de Taylor en el entorno del punto ![]() como sigue,
como sigue,
donde ![]() ,
, ![]() y
y ![]() son las componentes del desplazamiento en la dirección de los ejes
son las componentes del desplazamiento en la dirección de los ejes ![]() ,
, ![]() y
y ![]() , respectivamente.
, respectivamente.
Los términos del desarrollo de grado mayor a uno se han despreciado debido a la hipótesis de pequeñas deformaciones. La variación del vector
![]() que se muestra en la Figura 2.5 será:
que se muestra en la Figura 2.5 será:
Sustituyendo las expresiones (2.5) en (2.6) y desarrollando esta última, se obtiene:
Expresando (2.7) en forma matricial se tiene
Donde la``matriz" J se denomina tensor gradiente de desplazamientos. Dicho tensor se puede descomponer en un tensor simétrico y otro antisimétrico como sigue
siendo
![]() es el tensor de pequeñas deformaciones, que desarrollando sus componentes se tiene
es el tensor de pequeñas deformaciones, que desarrollando sus componentes se tiene
y
![]() es el tensor de rotación, que desarrollado tiene de componentes
es el tensor de rotación, que desarrollado tiene de componentes
La expresión (2.8) se puede expresar, en forma matricial, teniendo en cuenta (2.9) como
que coincide con la expresión (2.6), ésta expresada en forma vectorial.
La ecuación anterior implica que la variación relativa de la distancia entre dos puntos infinitamente próximos de un sólido elástico se puede expresar como suma de una componente de deformación y otra componente de giro, y
![]() , en forma matricial, puede expresarse como
, en forma matricial, puede expresarse como
En la Figura 2.6 a) los puntos ![]() y
y ![]() (vector
(vector
![]() ) han sufrido una traslación como sólido rígido hasta las posiciones
) han sufrido una traslación como sólido rígido hasta las posiciones ![]() y
y ![]() respectivamente, definida por el vector
respectivamente, definida por el vector
![]() . En la Figura 2.6 b) se produce una rotación como sólido rígido del segmento
. En la Figura 2.6 b) se produce una rotación como sólido rígido del segmento ![]() alrededor del punto
alrededor del punto ![]() , de valor
, de valor
![]() (
(
![]() ) (por la hipótesis de pequeños desplazamientos se aproxima el arco a la tangente).
) (por la hipótesis de pequeños desplazamientos se aproxima el arco a la tangente).
Finalmente, para pasar a la posición ![]() se produce una deformación del vector
se produce una deformación del vector
![]() de valor
de valor
![]() (
(
![]() ). En la Figura 2.7 se muestra la descomposición completa de la deformación en el entorno de un punto.
). En la Figura 2.7 se muestra la descomposición completa de la deformación en el entorno de un punto.