5.4.- Oscilaciones amortiguadas y forzadas
OSCILACIONES AMORTIGUADAS:
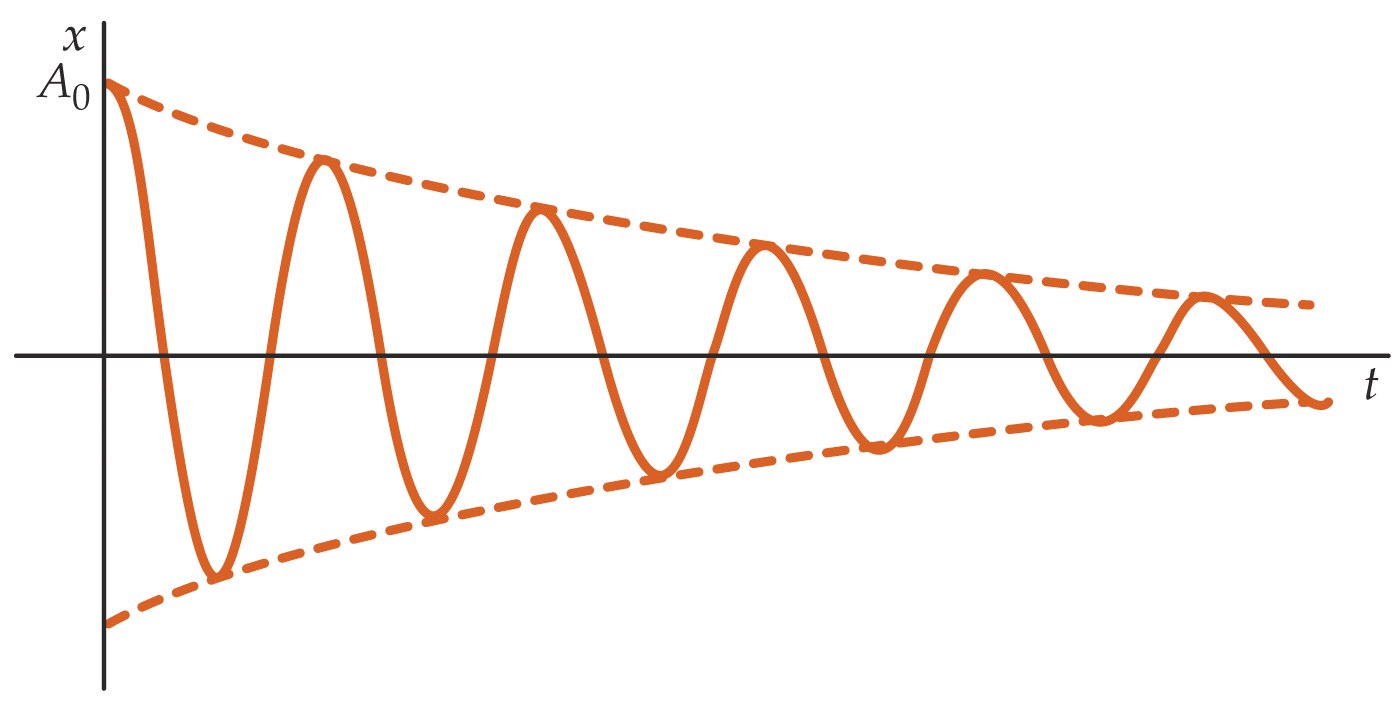
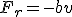 , la ecuación diferencial que tenemos es:
, la ecuación diferencial que tenemos es:
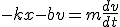
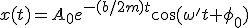
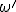 viene dada por:
viene dada por:
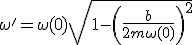
OSCILADOR FORZADO.
Puesto que las oscilaciones disminuyen gradualmente con el tiempo, para mantener un sistema oscilando es necesario suministrar energía al sistema. Cuando hacemos esto llamamos al oscilador 'forzado', como el que se representa en la figura:
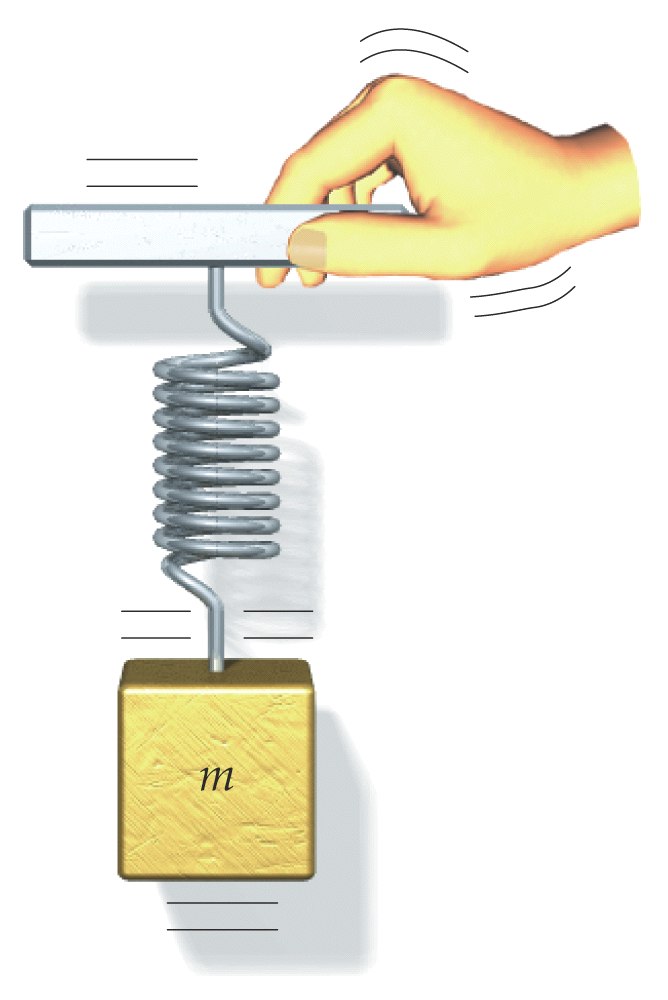
Para estudiar matemáticamente el oscilador forzado suponemos que está sujeto a la ley de Hooke, que además está amortiguado por un rozamiento en un fluido, y que está sujeto a una fuerza externa restauradora que varía armónicamente con el tiempo:
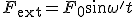
donde 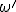 es la frecuencia angular de la fuerza, que en principio es distinta de la frecuencia angular natural del oscilador
es la frecuencia angular de la fuerza, que en principio es distinta de la frecuencia angular natural del oscilador 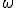 (si coinciden tenemos el fenómeno de la resonancia, en el que la energía absorbida del oscilador es máxima y llamamos a
(si coinciden tenemos el fenómeno de la resonancia, en el que la energía absorbida del oscilador es máxima y llamamos a 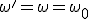 ). La ecuación diferencial del movimiento es en este caso:
). La ecuación diferencial del movimiento es en este caso:
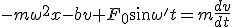
No vamos a resolver de manera exacta esta ecuación diferencial, pero sí lo haremos cualitativamente. La solución consta de dos partes. Una de ellas es una solución transitoria que desparece con el tiempo y que no tendremos en cuenta, y otra parte es una solución estacionaria que permenece en el tiempo. La solución estacionaria se puede escribir como:
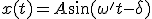
Si la frecuencia externa 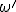 es igual a la natural del sistema
es igual a la natural del sistema 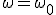 entonces la amplitud es muy grande (no entramos en detalles del valor de la amplitud A ni de la fase
entonces la amplitud es muy grande (no entramos en detalles del valor de la amplitud A ni de la fase 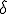 ).
).
Completa la siguiente tabla:
|
Número de fuerzas |
Ecuación diferencial |
Solución a la ecuación diferencial
|
Otras características (Opcional) |
||
|
Oscilador armónico simple |
|||||
|
Oscilador amortiguado
|
|||||
|
Oscilador forzado
|

Física I by Esther Jódar Ferrández, José Luis Sánchez Méndez is licensed under a Creative Commons Reconocimiento-NoComercial-CompartirIgual 3.0 Unported License.
Based on a work at ocw.bib.upct.es.