5.3.- Movimiento armónico simple.
- Ecuación:
En el apartado anterior hemos visto la ecuación de la dinámica del movimiento de un muelle. Si escribimos en esta ecuación la segunda ley de Newton junto con la definición de aceleración obtenemos la ecuación diferencial que rige el movimiento armónico simple:
,
se puede demostrar que una solución de esta ecuación es:
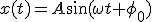 Para demostrar que es solución de la ecuación diferencial derivamos dos veces para obtener la aceleración:
Para demostrar que es solución de la ecuación diferencial derivamos dos veces para obtener la aceleración: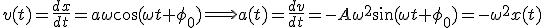
Sustituyendo en la ecuación diferencial las expresiones de a(t) y x(t):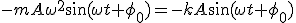
Expresión que simplificada se cumple con tal de que 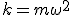 .
.
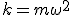 .
. Repite todo el procedimiento anterior para el caso del péndulo. Tendrás que sustituir x por s y k por mg/L. En la demostración obtendrás una de las expresiones utilizadas para una de las prácticas de laboratorio, ¿cuál?
- Energía:
La energía mecánica es suma de la energía cinética y potencial. Teniendo en cuenta las expresiones obtenidas en la demostración anterior tenemos que: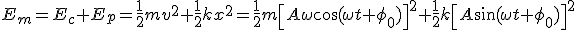 Asociamos los términos teniendo en cuenta que
Asociamos los términos teniendo en cuenta que:
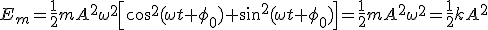
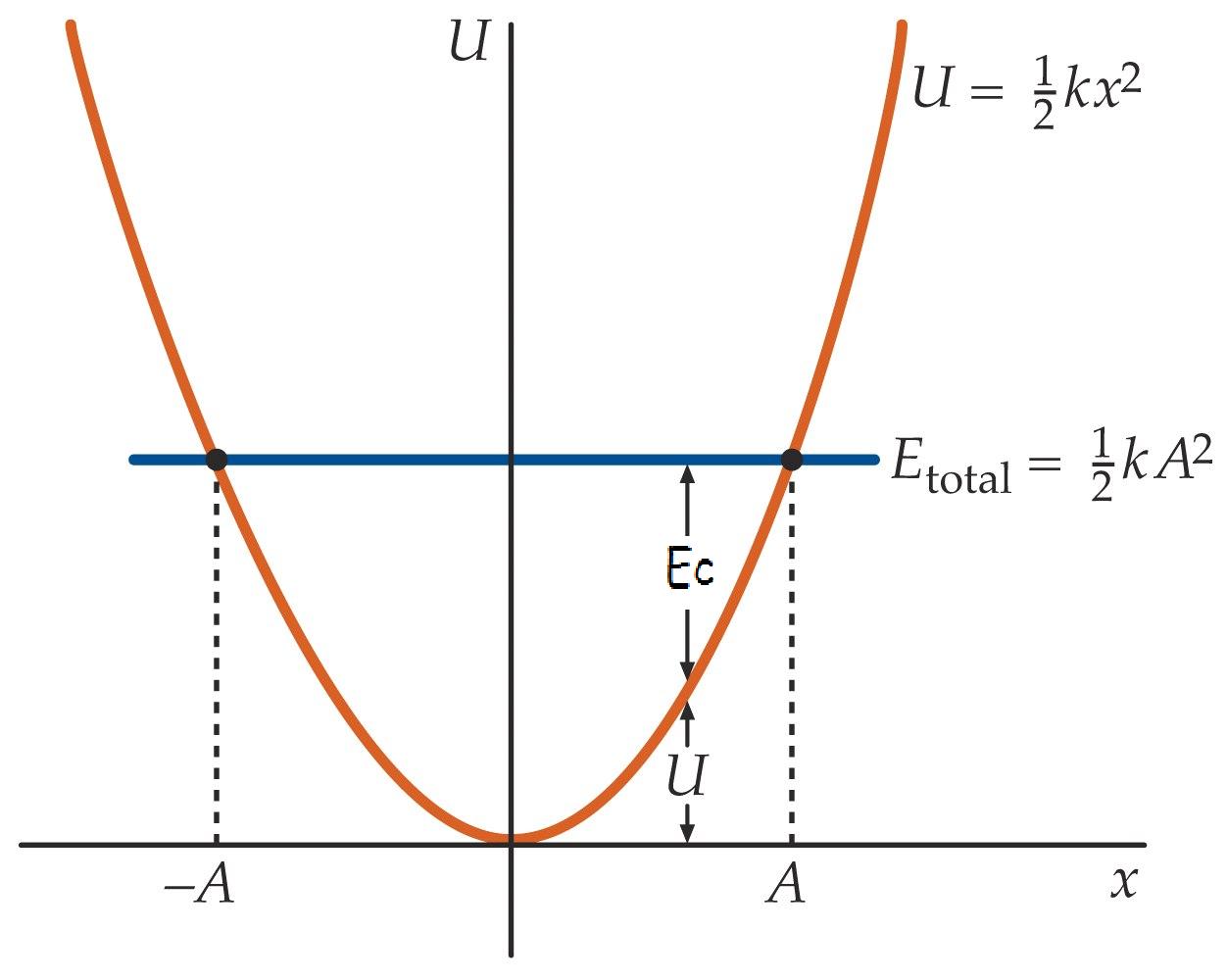
Explica la gráfica resaltando las transformaciones energéticas que suceden desde -A hasta A. Además, trata de asociar cada punto con el estado de movimiento del oscilador.

Física I by Esther Jódar Ferrández, José Luis Sánchez Méndez is licensed under a Creative Commons Reconocimiento-NoComercial-CompartirIgual 3.0 Unported License.
Based on a work at ocw.bib.upct.es.