Compresión excéntrica de una barra esbelta

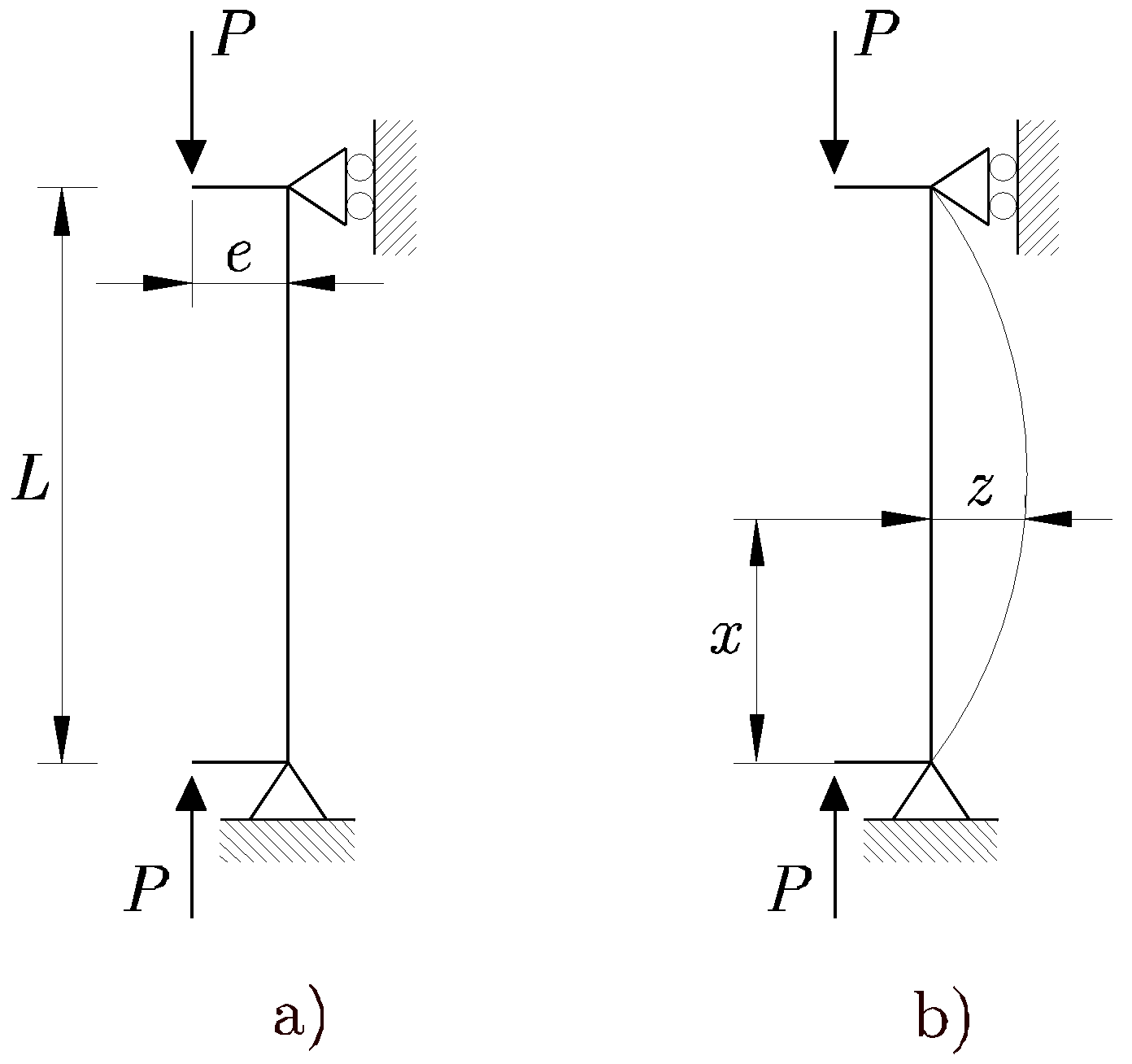
Sea la barra considerada en el caso fundamental sometida a una carga con excentricidad e, como se muestra en la Figura 15.10 a).

**Figura 15.10:** Compresión excéntrica de una barra esbelta

Al flexionarse la barra, como se muestra en la Figura 15.10 b), se origina en cada sección de la misma un momento flector de valor

$\displaystyle M_y\left(x\right)=P(e+z)$

(15.24)

La ecuación diferencial de la curva elástica, considerando pequeños desplazamientos, es

$\displaystyle E\hspace{0.5mm}I_y\hspace{0.5mm}z''=-M_y\left(x\right)=-P(e+z)$

(15.25)

Haciendo 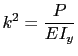$k^2=\displaystyle\frac{P}{EI_y}$ , la ecuación (15.25) queda como

$\displaystyle z''+k^2z=-k^2e$

(15.26)

La solución general de la ecuación (15.26) es

$\displaystyle z=C_1$ sen $\displaystyle \hspace{0.15mm}\left(kx\right)+C_2 \cos\left(kx\right)-e$

(15.27)

Las constantes y se calculan a partir de las condiciones de contorno.

	$\displaystyle x=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} C_2=e\vspace{0.25cm}$	(15.28)
	$\displaystyle x=L \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z=0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} C_1$ sen $\displaystyle \hspace{0.15mm}\left(kL\right)+e\left(\cos\left(kL\right)-1\right)=0$	(15.29)

De (15.29) se obtiene que

$\displaystyle C_1=e\displaystyle\frac{\cos\left(kL\right)-1}{\text{sen}\hspace{0.15mm}\left(kL\right)}=e\tan \left(k\frac{L}{2}\right)$

(15.30)

La ecuación de la curva eslástica es

$\displaystyle z=e\tan \left(k\frac{L}{2}\right)$ sen $\displaystyle \hspace{0.15mm}\left(kx\right)+e \cos\left(kx\right)-e$

(15.31)

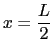El momento flector máximo se produce en la sección de $z_{\text{m\'{a}x}}$ , y ésta se produce en $x=\displaystyle\frac{L}{2}$ .

$\displaystyle z_{\text{m\'{a}x}}=e\tan \left(k\frac{L}{2}\right) \hspace{0.5mm}... ...L}{2}\right)+e \cos\left(k\frac{L}{2}\right)-e=e\sec\left(k\frac{L}{2}\right)-e$

(15.32)

Siendo el momento flector máximo

$\displaystyle M_{y_{\text{m\'{a}x}}}=P(e+z)=Pe\sec\left(k\frac{L}{2}\right)$

(15.33)

Se observa que el momento flector obtenido es el momento flector de primer orden multiplicado por el coeficiente $\sec\left(k\frac{L}{2}\right)$ . Cuando se alcance la carga crítica, el valor de la secante se hace infinito

$\begin{displaymath}\begin{array}{c} \sec\left(k\displaystyle\frac{L}{2}\right)=... ...\sec\left(\displaystyle\frac{\pi}{2}\right)=\infty \end{array}\end{displaymath}$

(15.34)