Estabilidad

Los tres tipos de equilibrio que puede presentar un cuerpo son:

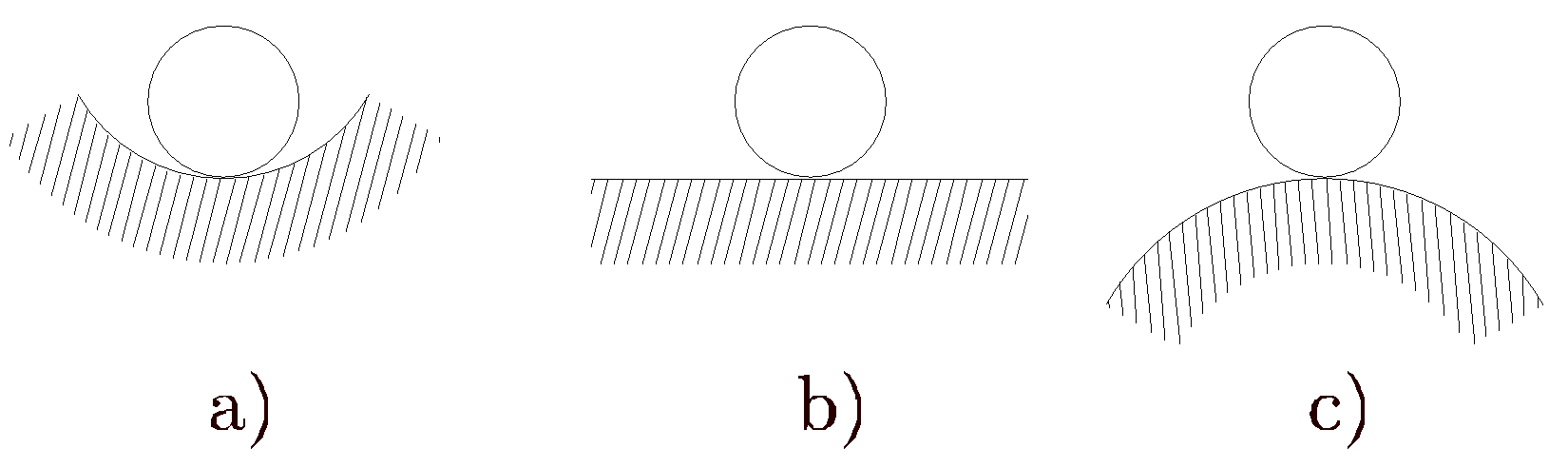
Sea una esfera apoyada sobre una superficie cóncava, sobre una superficie plana, y sobre una superficie convexa, tal como se muestra en la Figura 15.1. Si la esfera de la Figura 15.1 a) se desplaza una magnitud infinitamente pequeña de su posición de equilibrio inicial, ésta retorna a la posición original (equilibrio estable). Si dicho desplazamiento lo realiza la esfera de la Figura 15.1 b), ésta conserva su posición de equilibrio (equilibrio indiferente). Por último, al provocar el desplazamiento de la esfera de la Figura 15.1 c), ésta se alejará cada vez más de su posición de equilibrio inicial (equilibrio inestable).

Figura 15.1: Tipos de equilibrio. a) Equilibrio estable. b) Equilibrio indiferente c) Equilibrio inestable
Image 01-Pandeo

Se entiende por estabilidad la propiedad de un sistema estructural de mantener su estado de equilibrio durante el periodo de actuación de las fuerzas exteriores. Si se considera la esfera y la superficie de rodadura anteriores como un sistema estructural, en los casos a y b se dice que el sistema es estable. En el caso c se dice que el sistema es inestable.

El análisis de estabilidad de los sistemas elásticos permite establecer aquellos valores de las fuerzas exteriores para los que el equilibrio estable se convierte en inestable. Estas fuerzas reciben el nombre de fuerzas críticas.

Se aclararán estos conceptos con un ejemplo sencillo recogido de la Mecánica Clásica. Sea la barra rígida AB, articulada sobre un apoyo fijo en A y sostenida en posición vertical por un resorte, como se muestra en la Figura 15.2 a).

Figura: 15.2 Tipos de equilibrio. Estudio de la estabilidad del equilibrio de una barra articulada y mantenida en posición vertical por un resorte
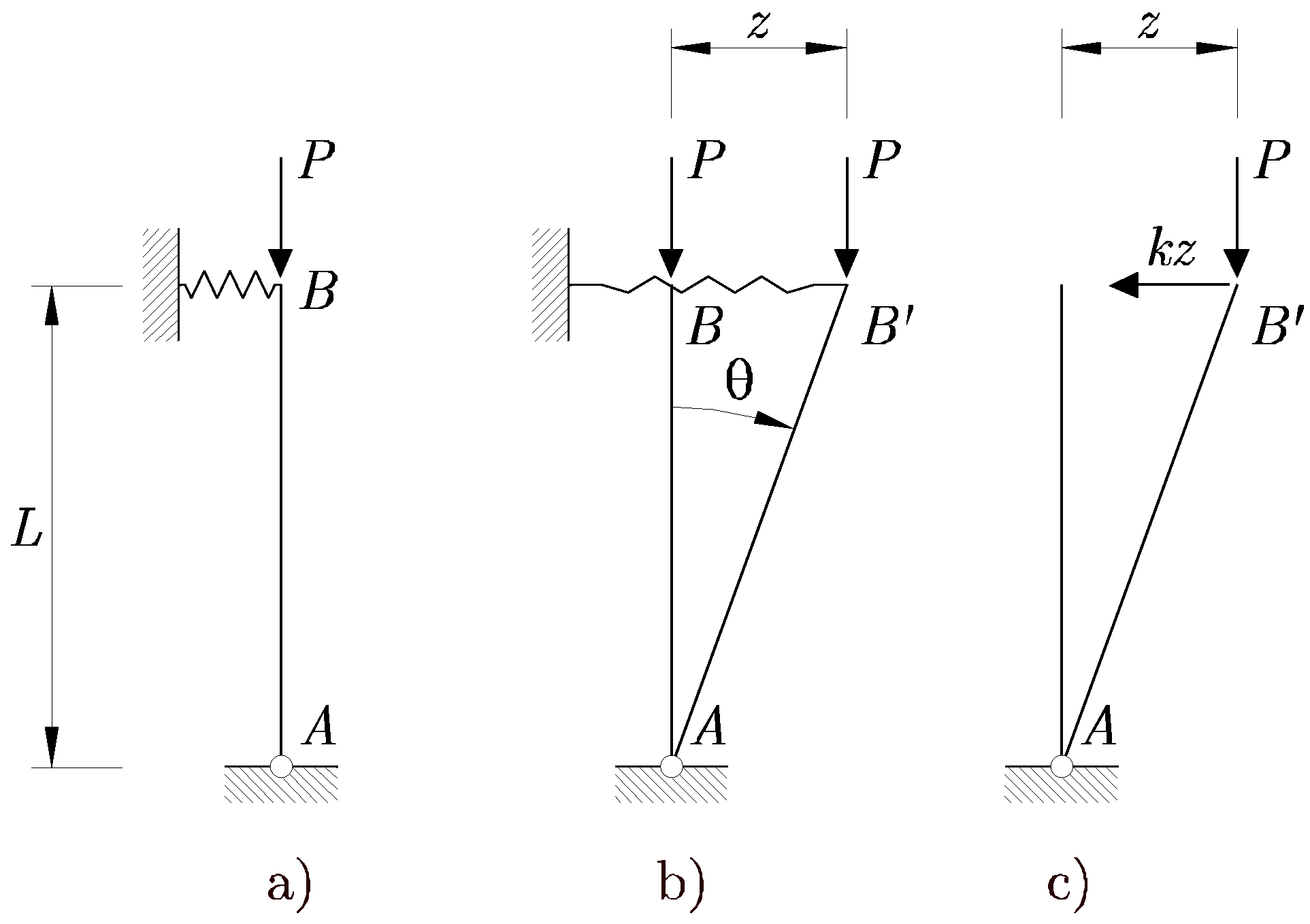Image 02-Pandeo

Si se separa el punto B de su posición de equilibrio una longitud $ BB' = z$, el resorte ejerce sobre el extremo superior de la barra una fuerza horizontal $ k\hspace{0.5mm} z$, siendo k la rigidez del resorte. Se estudiará la estabilidad del sistema bajo la acción de una fuerza vertical P aplicada en B, y dirigida hacia abajo. Para ello se considerará la barra en una posición $ AB'$ próxima a la de equilibrio vertical, como se muestra en la Figura 15.2 b).

La fuerza P produce un momento $ P\hspace{0.5mm}z$ respecto al punto A, en sentido horario, que tiende a alejar la barra de su posición de equilibrio. Por otro lado, el momento respecto al punto A de la fuerza ejercida por el resorte es $ k\hspace{0.5mm}z\hspace{0.5mm}L$, en sentido antihorario, y tiende a devolver a la barra a su posición de equilibrio, como se muestra en la Figura 15.2 c).

Así pues, el equilibrio de la barra en la posición vertical es estable si se cumple que

$\displaystyle k\hspace{0.5mm}z\hspace{0.5mm}L>P\hspace{0.5mm}z \hspace{0.5cm} K\hspace{0.5mm}L>P$ (15.1)

Es decir, P debe ser menor a un valor crítico $ P_{\text{cr\'{\i}t}}=K\hspace{0.5mm}L$. Si se supera dicho valor, el sistema pierde la estabilidad. Cuando $ P=P_{\text{cr\'{\i}t}}$, el equilibrio de la barra es indiferente.

El caso más simple de pérdida de estabilidad en cuerpos elásticos corresponde a una barra comprimida axialmente, como la que se muestra en la Figura 15.3. Cuando la carga aplicada es lo suficientemente grande, la barra no puede mantener su forma recta y se flexiona, dando lugar a la pérdida de estabilidad.

Figura: 15.3 Pérdida de la estabilidad de una barra carga axialmente
Image 03-Pandeo