Plastificación parcial de la sección
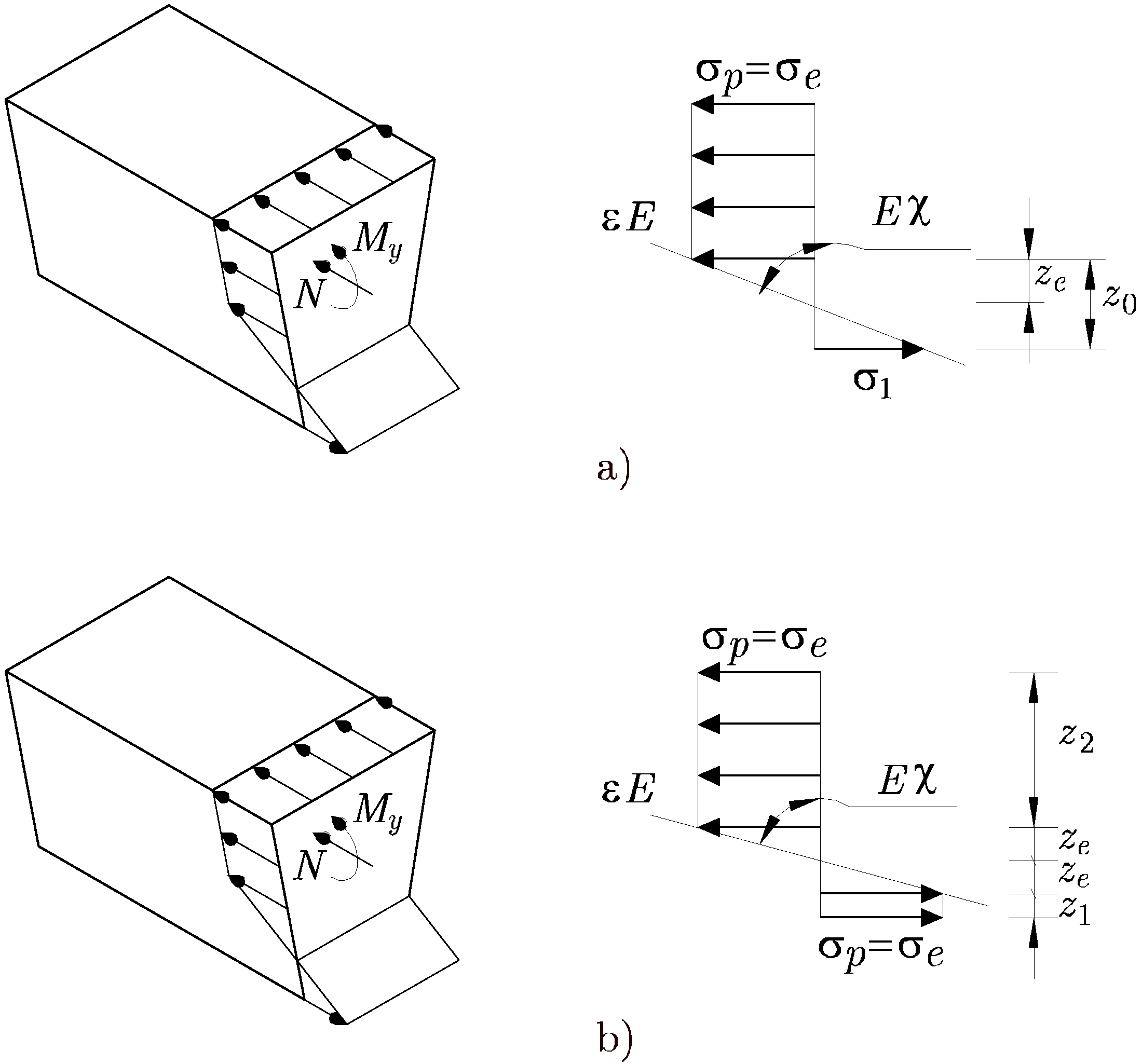
Se trata de obtener la distribución de tensiones y la curvatura en una sección solicitada a flexión compuesta (se entiende que el axil es de compresión), sin que la sección se agote (plastifique totalmente). En la Figura 12.11 se muestran la dos posibilidades:
- Sólo una cabeza de la sección ha plastificado, como se muestra en la Figura 12.11 a). Las incógnitas son
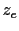 y
y 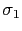 .
.
- Las dos cabezas de la sección han plastificado, como se muestra en la Figura 12.11 b). Las incógnitas son
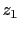 y
y 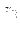 .
.
Para el primer caso, alcanzará antes la plastificación aquella cabeza que según las ecuaciones clásicas de la resistencia de materiales esté más tensionada.
Las deformaciones en la sección se obtienen teniendo en cuenta que la inclinación del diagrama de tensiones en la parte elástica es
![]() y que
y que
![]() .
.
Dependiendo de la complicación de la sección, para determinar la distribución de tensiones puede ser necesario recurrir a métodos iterativos. Se parte de una distribución que se va corrigiendo hasta conseguir que los valores de ![]() y
y ![]() de la i-ésima iteración coincidan con los N y M que solicitan a la sección. Hay que tener en cuenta a la hora de establecer los incrementos para iterar, que un incremento en la curvatura produce un aumento en el momento, y que un desplazamiento del eje neutro hacia la zona de tracción, produce un aumento del axil.
de la i-ésima iteración coincidan con los N y M que solicitan a la sección. Hay que tener en cuenta a la hora de establecer los incrementos para iterar, que un incremento en la curvatura produce un aumento en el momento, y que un desplazamiento del eje neutro hacia la zona de tracción, produce un aumento del axil.
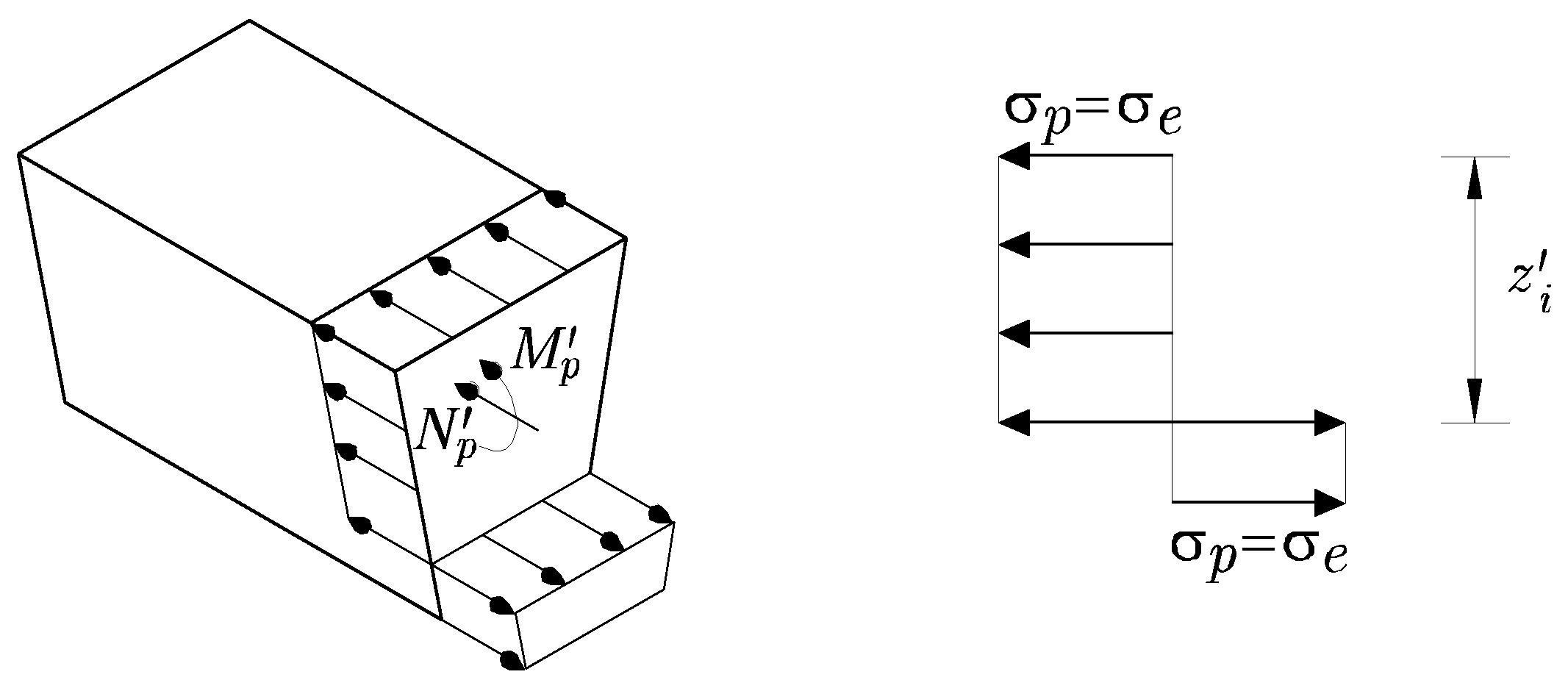
Plastificación total de la sección
Se trata de obtener las parejas de valores ![]() y
y ![]() que agotan la sección dando lugar a una distribución de tensiones como la mostrada en la Figura 12.12.
que agotan la sección dando lugar a una distribución de tensiones como la mostrada en la Figura 12.12.
Con las distintas parejas de valores ![]() y
y ![]() que agotan la sección, se construye el diagrama de interacción de la sección, que se muestra en la Figura 12.13 a). Éste se genera determinando para distintos valores de profundidad del eje neutro,
que agotan la sección, se construye el diagrama de interacción de la sección, que se muestra en la Figura 12.13 a). Éste se genera determinando para distintos valores de profundidad del eje neutro, ![]() , los valores de
, los valores de
![]() y
y
![]() que agotan la sección. Estos valores se representan en un sistema de ejes, de abscisas
que agotan la sección. Estos valores se representan en un sistema de ejes, de abscisas ![]() y ordenadas
y ordenadas ![]() .
.
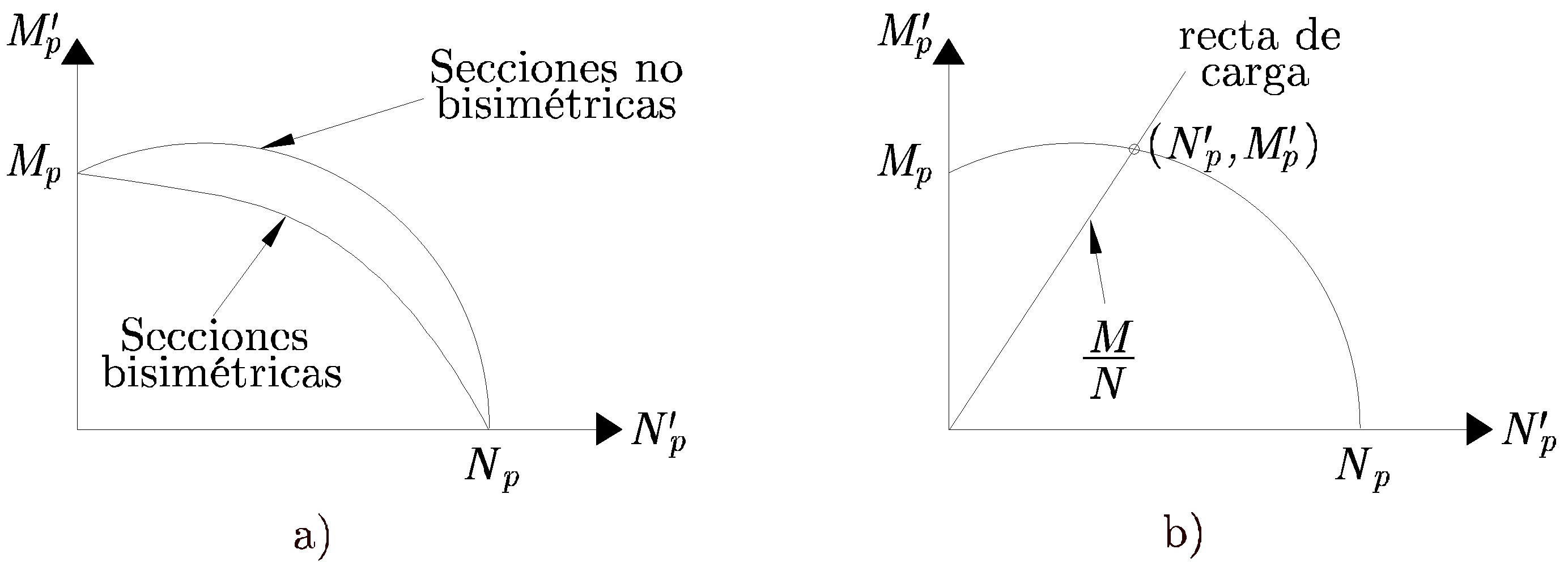 |
En la Figura 12.13 a) se han representado sendos diagramas de interacción correspondientes a una sección bisimétrica y a una sección no bisimétrica. En secciones bisimétricas el valor máximo de ![]() coincide con
coincide con ![]() . En secciones no bisimétricas, el valor máximo de
. En secciones no bisimétricas, el valor máximo de ![]() es superior al momento plástico de la sección,
es superior al momento plástico de la sección, ![]() .
.
A partir del diagrama de interacción es posible obtener la carga de agotamiento para una sección. Para ello se traza la recta que pasa por el origen y tiene de pendiente
![]() (siendo M y N las solicitaciones sobre la sección). La intersección de dicha recta con el diagrama de interacción da el valor de los esfuerzos críticos, tal y como se muestra en la Figura 12.13 b).
(siendo M y N las solicitaciones sobre la sección). La intersección de dicha recta con el diagrama de interacción da el valor de los esfuerzos críticos, tal y como se muestra en la Figura 12.13 b).