Secciones sin zona de tracción

Hay materiales cuya resistencia a tracción es tan pequeña que no es considerada en los cálculos. Para el caso de elementos construidos con estos materiales y que van a estar sometidos a un axil excéntrico, es necesario conocer la posición del eje neutro que separa la zona de la sección que trabaja (zona comprimida) de la que no trabaja (zona traccionada).

**Figura 10.6:** Determinación del núcleo central

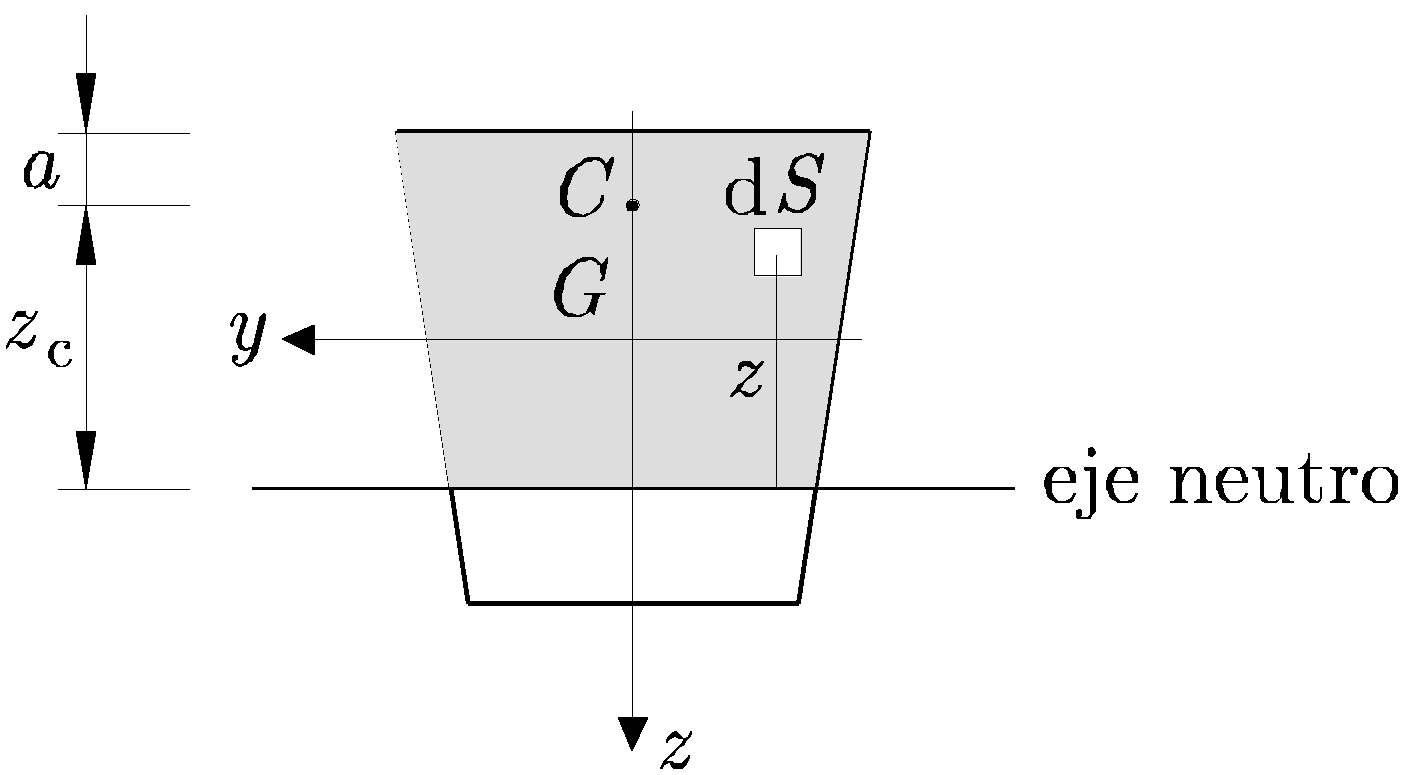
Sea una sección genérica, con eje de simetría coincidente con el eje z. Se supondrá que el esfuerzo axil N actúa en el punto C, sobre el eje de simetría, a una distancia a del borde y fuera del núcleo central, como se muestra en la Figura 10.6.

La sección está sometida a flexión compuesta según el eje y. Por tanto, el eje neutro es perpendicular al eje z. Como se ha visto en apartados anteriores, las tensiones normales son proporcionales a su distancia al eje neutro. Así, un elemento diferencial dS, a una distancia z del eje neutro, tendrá como tensión $\sigma=kz$ .

Para determinar la distancia del punto de actuación del axil al eje neutro, , se establecen las condiciones de equilibrio de fuerzas y de momentos. Así, la resultante de las tensiones que actúan en la zona activa (sombreada en la figura) ha de ser igual al esfuerzo axil $N\left(x\right)$ :

$\displaystyle N\left(x\right)=\int_S\sigma_x$ d $\displaystyle S=\int_Sk\hspace{1mm}z$ d $\displaystyle S=k\int_Sz$ d $\displaystyle S=k\hspace{1mm}Q_{en}$

(10.13)

siendo $Q_{en}$ el momento estático de la zona comprimida respecto al eje neutro.

Además ha de verificarse que el momento de la resultante de las tensiones de compresión respecto al eje neutro ha de ser igual al momento del axil respecto a dicho eje.

$\displaystyle N\left(x\right)\hspace{1mm}z_c=\int_Sz\hspace{1mm}\sigma_x$ d $\displaystyle S=\int_Sk\hspace{1mm}z^2$ d $\displaystyle S=k\int_Sz^2$ d $\displaystyle S=k\hspace{1mm}I_{en}$

(10.14)

siendo $I_{en}$ el momento de inercia de la zona comprimida respecto al eje neutro. Dividiendo (10.14) por (10.13) se obtiene

$\displaystyle z_c=\displaystyle\frac{I_{en}}{Q_{en}}$

(10.15)

Los valores de $Q_{en}$ e $I_{en}$ son función de la incógnita . Por tanto, resolviendo la ecuación resultante, se determina la posición del eje neutro referida al punto de aplicación del axil.