Cambio de sistema de referencia

Conocido el tensor de tensiones, el vector tensión $ \overrightarrow{t^{\text{n}}}$ sobre un plano de normal $ \overrightarrow{n}$ viene dado por la fórmula de Cauchy (en notación matricial)

$\displaystyle \textbf{t}^{\text{\textbf{n}}}=\boldsymbol{\sigma} \text{\textbf{n}}$    

Las componentes del tensor de tensiones están referidas a un sistema de referencia $ xyz$ como se muestra en la Figura 3.10 a).

Figura 3.10: a) Componentes de la tensión referidas a un sistema $ xyz$. b) Componentes de la tensión referidas a un sistema $ x^*y^*z^*$
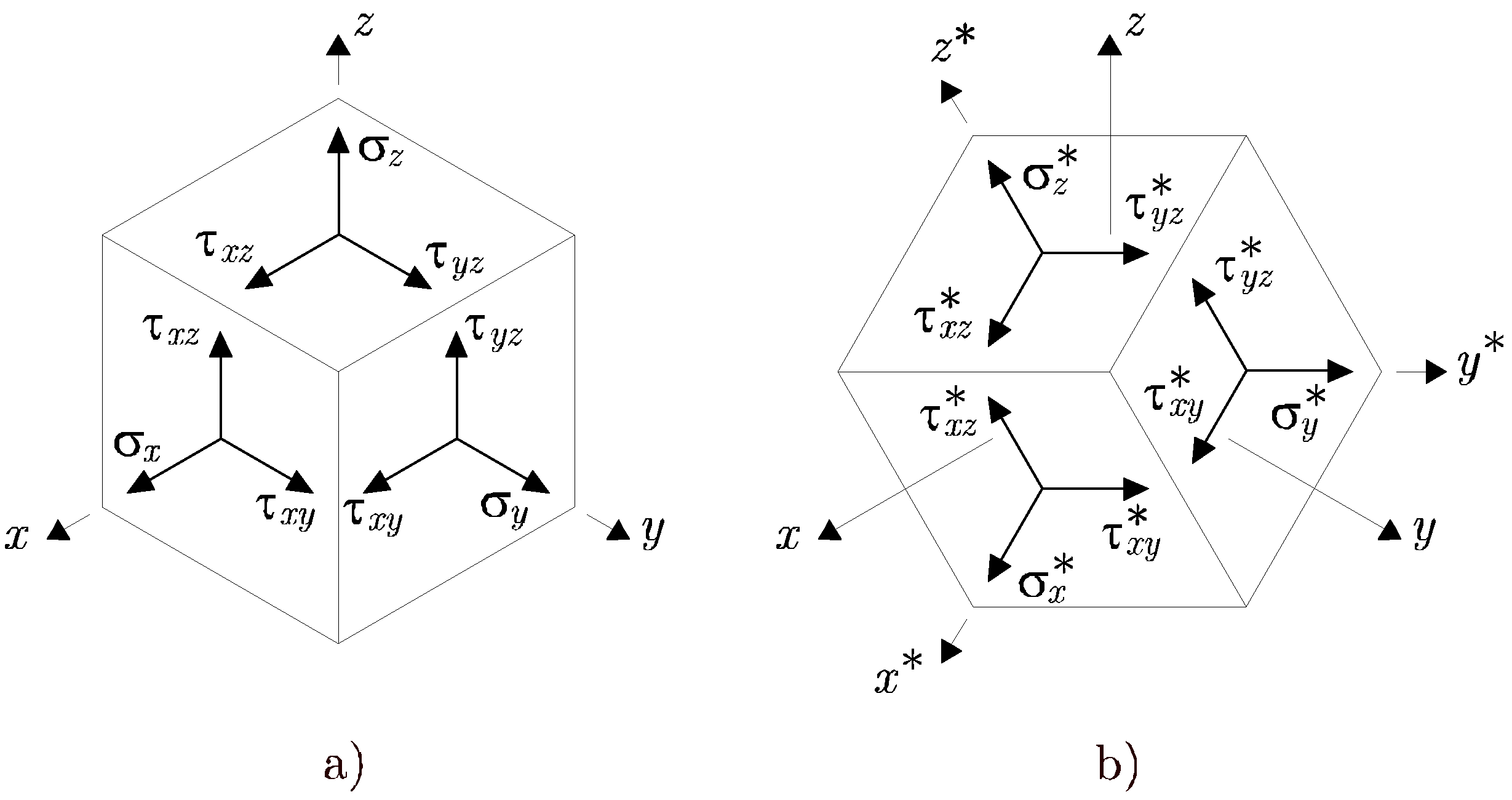Image 10-Tensiones

Se considerará un nuevo sistema de referencia ortogonal con el mismo origen que el anterior, pero con distinta orientación como se muestra en la Figura 3.10 b). ¿Cuáles serán las componentes del tensor de tensiones en este nuevo sistema?

En lo que sigue de apartado se utilizará notación matricial. Sea $ \boldsymbol{\sigma^*}$ el tensor de tensiones referido a este nuevo sistema. El vector tensión t$ ^$n*, correspondiente a un plano cuya orientación viene definida por el vector unitario $ \textbf{n}^\textbf{*}$, es

$\displaystyle \textbf{t}^\textbf{n*}=\boldsymbol{\sigma}^* \textbf{n}^\textbf{*}$ (3.22)

Los vectores tensión en ambos sistemas, referidos al mismo plano, están relacionados mediante la matriz de rotación de ejes R por la ecuación

$\displaystyle \textbf{t}^{\textbf{n*}}=\textbf{R}\hspace{1mm} \textbf{t}^{\textbf{n}}$ (3.23)

Las filas de la matriz de rotación de ejes son los cosenos de los ángulos formados por cada eje nuevo con los antiguos, medidos en sentido antihorario del antiguo al nuevo sistema,

R$\displaystyle =\left( \begin{array}{ccc} \cos \theta_{xx^*} & \cos \theta_{yx... ...heta_{xz^*} & \cos \theta_{yz^*} & \cos \theta_{zz^*} \\ \end{array} \right)$ (3.24)

Las componentes de los vectores unitarios en ambos sistemas de referencia están ligadas por la relación

n*$\displaystyle = \textbf{R} \hspace{1mm} \textbf{n}$ (3.25)

Al ser la matriz de cambio de ejes ortogonal (por pasar de un sistema de coordenadas ortogonal dextrógiro a otro sistema de coordenadas ortogonal dextrógiro), su inversa es igual a la traspuesta, R$ ^{-1}=$R$ ^$T. Por tanto, se cumple

n$\displaystyle =$   R$\displaystyle ^{-1} \textbf{n}^\textbf{*}=$   R$\displaystyle ^$T$\displaystyle \textbf{n}^\textbf{*}$ (3.26)

Teniendo en cuenta las expresiones (3.21), (3.22), (3.23) y (3.24), se tiene

t$\displaystyle ^$n*$\displaystyle =$   R   t$\displaystyle ^$n$\displaystyle =$   R$\displaystyle \hspace{1mm} \boldsymbol{\sigma}$   n$\displaystyle =$   R$\displaystyle \boldsymbol{\sigma}$   R$\displaystyle ^$T$\displaystyle \textbf{n}^\textbf{*}$ (3.27)

Es decir

$\displaystyle \boldsymbol{\sigma}^*\textbf{n}^\textbf{*}=\textbf{R} \hspace{1mm} \boldsymbol{\sigma} \textbf{R}^\textbf{T} \textbf{n}^\textbf{*}$ (3.28)

y dividiendo por $ \textbf{n}^\textbf{*}$

$\displaystyle \boldsymbol{\sigma^*}= \textbf{R} \hspace{1mm} \boldsymbol{\sigma} \textbf{R}^\textbf{T}$ (3.29)

La ecuación (3.29) permite obtener el tensor de tensiones en cualquier sistema de referencia conocidos el tensor en otro sistema de referencia y la matriz de rotación de ejes entre ambos sistemas.