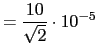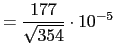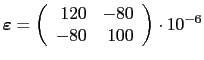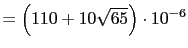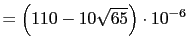Ejercicios propuestos - Tema 2: Deformaciones
Ejercicio 1
El campo vectorial de desplazamientos en el entorno del punto  de un medio continuo es
de un medio continuo es
siendo las unidades en milímetros.
Se pide:
- Calcular el tensor de pequeñas deformaciones
- Calcular el tensor de rotación
Solución:
- Calcular el tensor de pequeñas deformaciones:
- Calcular el tensor de rotación:
Ejercicio 2
Conociéndose el tensor de pequeñas deformaciones
 en el entorno de un punto de un sólido elástico, se pide:
en el entorno de un punto de un sólido elástico, se pide:
- Calcular las componentes intrínsecas de la deformación del vector
Datos:
siendo
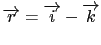 .
.
Solución:
- Calcular las componentes intrínsecas de la deformación del vector
Ejercicio 3
Conociéndose el tensor de pequeñas deformaciones
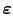 en el entorno de un punto de un sólido elástico trabajando a deformación plana, se pide:
en el entorno de un punto de un sólido elástico trabajando a deformación plana, se pide:
- Calcular las deformaciones principales
- Calcular las direcciones principales de deformación
Datos:
Solución:
- Calcular las deformaciones principales:
- Calcular las direcciones principales de deformación:
![]() de un medio continuo es
de un medio continuo es
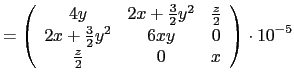
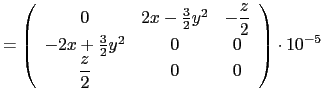
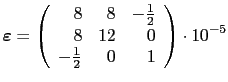
![]() .
.