Ejercicios propuestos - Tema 1: Conceptos e hipótesis fundamentales
Ejercicio 1
Una barra de sección transversal cilíndrica de un determinado material ha sido sometida a un ensayo de tracción. En la Tabla 1.1 se indican los valores obtenidos en dicho ensayo.
Obtener:
- Construir la gráfica
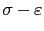
- Determinar gráficamente el valor límite de
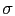 a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
- Determinar gráficamente los valores de
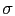 para
para
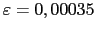 , asumiendo que el material se comporta linealmente para ese valor de
, asumiendo que el material se comporta linealmente para ese valor de
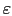 y considerando un comportamiento no lineal del material
y considerando un comportamiento no lineal del material
Datos:
Tabla 1.1:
Valores obtenidos del ensayo de tracción
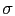 (MPa) (MPa) |
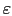 |
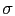 (MPa) (MPa) |
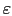 |
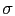 (MPa) (MPa) |
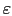 |
| [0.1mm]1-6
0,0 |
0,00 |
129,0 |
0,36 |
165,0 |
0,72 |
| 18,0 |
0,04 |
133,0 |
0,40 |
169,0 |
0,76 |
| 36,0 |
0,08 |
137,0 |
0,44 |
173,0 |
0,80 |
| 54,0 |
0,12 |
141,0 |
0,48 |
169,0 |
0,84 |
| 72,0 |
0,16 |
145,0 |
0,52 |
165,0 |
0,88 |
| 90,0 |
0,20 |
149,0 |
0,56 |
161,0 |
0,92 |
| 108,0 |
0,24 |
153,0 |
0,60 |
157,0 |
0,96 |
| 121,0 |
0,28 |
157,0 |
0,64 |
153,0 |
1,00 |
| 125,0 |
0,32 |
161,0 |
0,68 |
|
|
| |
|
|
|
|
|
Solución:
- Construir la gráfica
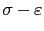
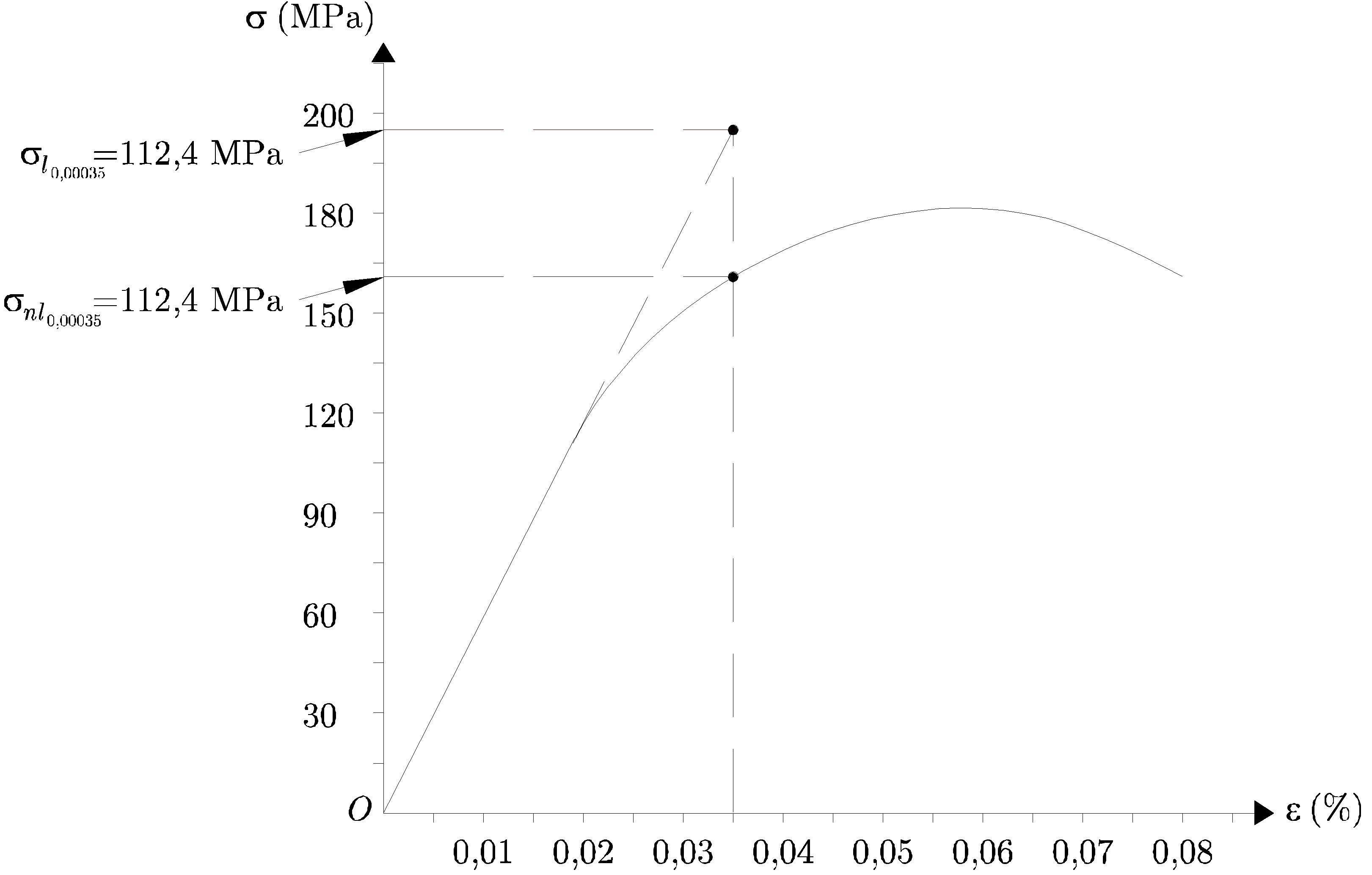
- Se muestra la gráfica en la Figura 1.7
Figura 1.7:
Diagrama tensión-deformación
|
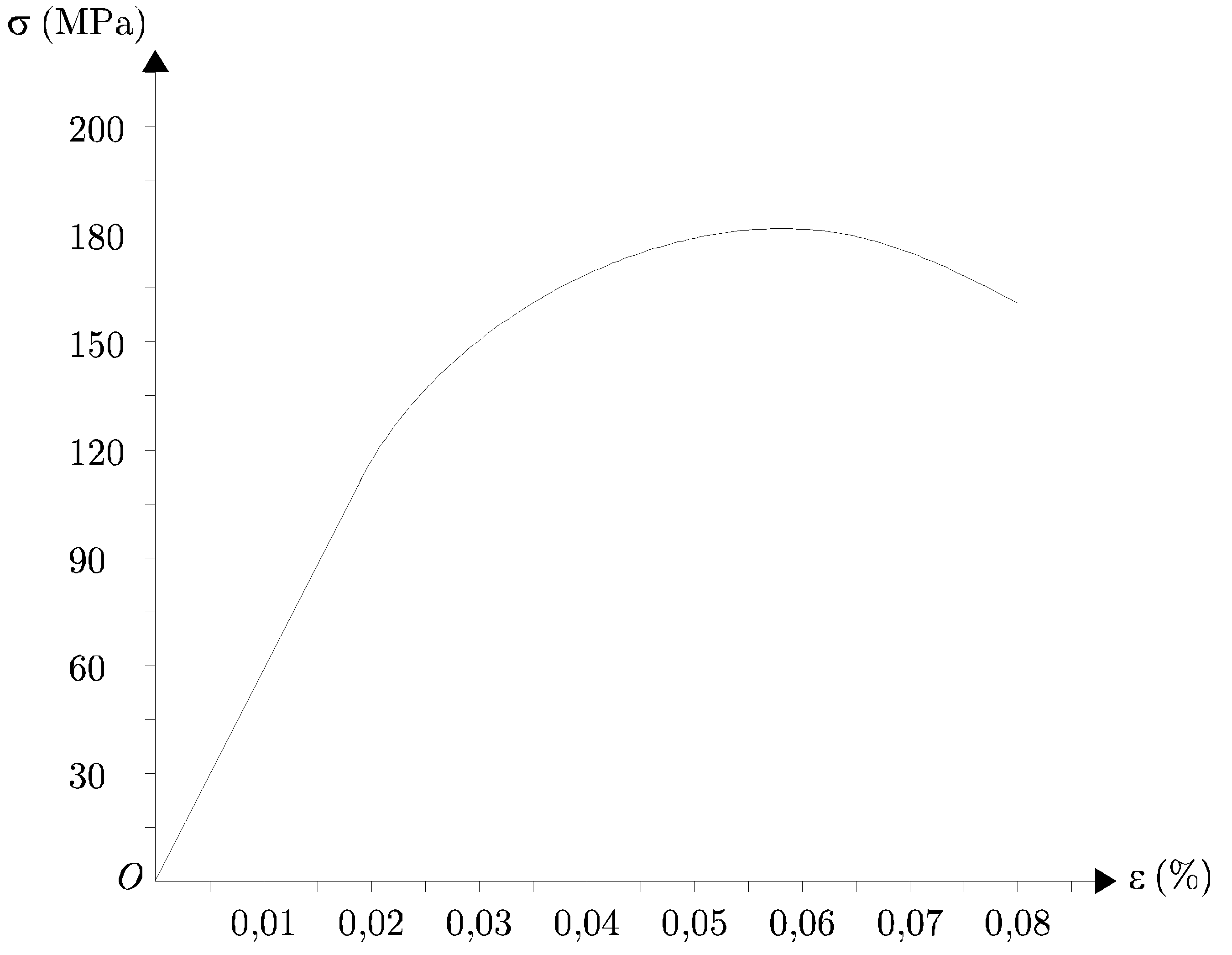 |
- Determinar gráficamente el valor límite de
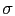 a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
- La Figura 1.8 muestra el valor límite de
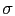 en el que el material deja de comportarse linealmente
en el que el material deja de comportarse linealmente
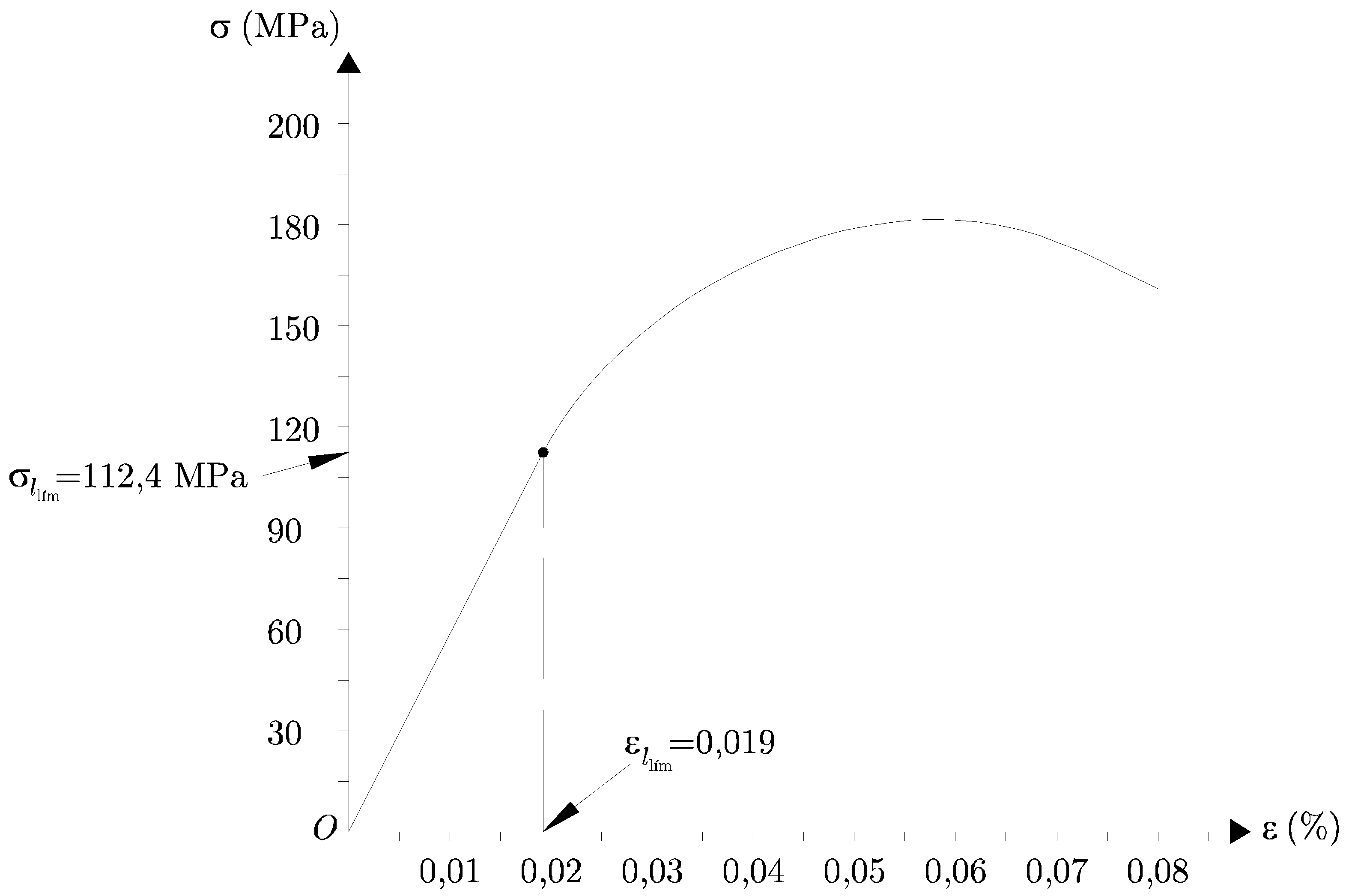
Figura 1.8:
Determinación gráfica del valor límite de 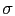 a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
a partir del cual el material deja de comportarse linealmente y la deformación correspondiente
|
 |
- Determinar gráficamente los valores de
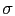 para
para
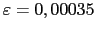 , asumiendo que el material se comporta linealmente para ese valor de
, asumiendo que el material se comporta linealmente para ese valor de
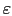 y considerando un comportamiento no lineal del material
y considerando un comportamiento no lineal del material
- La Figura 1.9 muestra los valores solicitados
Ejercicio 2
Para la viga en el voladizo que se muestra en la Figura 1.10 a) se conocen los desplazamientos del punto A para los estados de cargas que se muestran en la Figura 1.10 b).
Figura 1.10:
Aplicación del Principio de Superposición
|
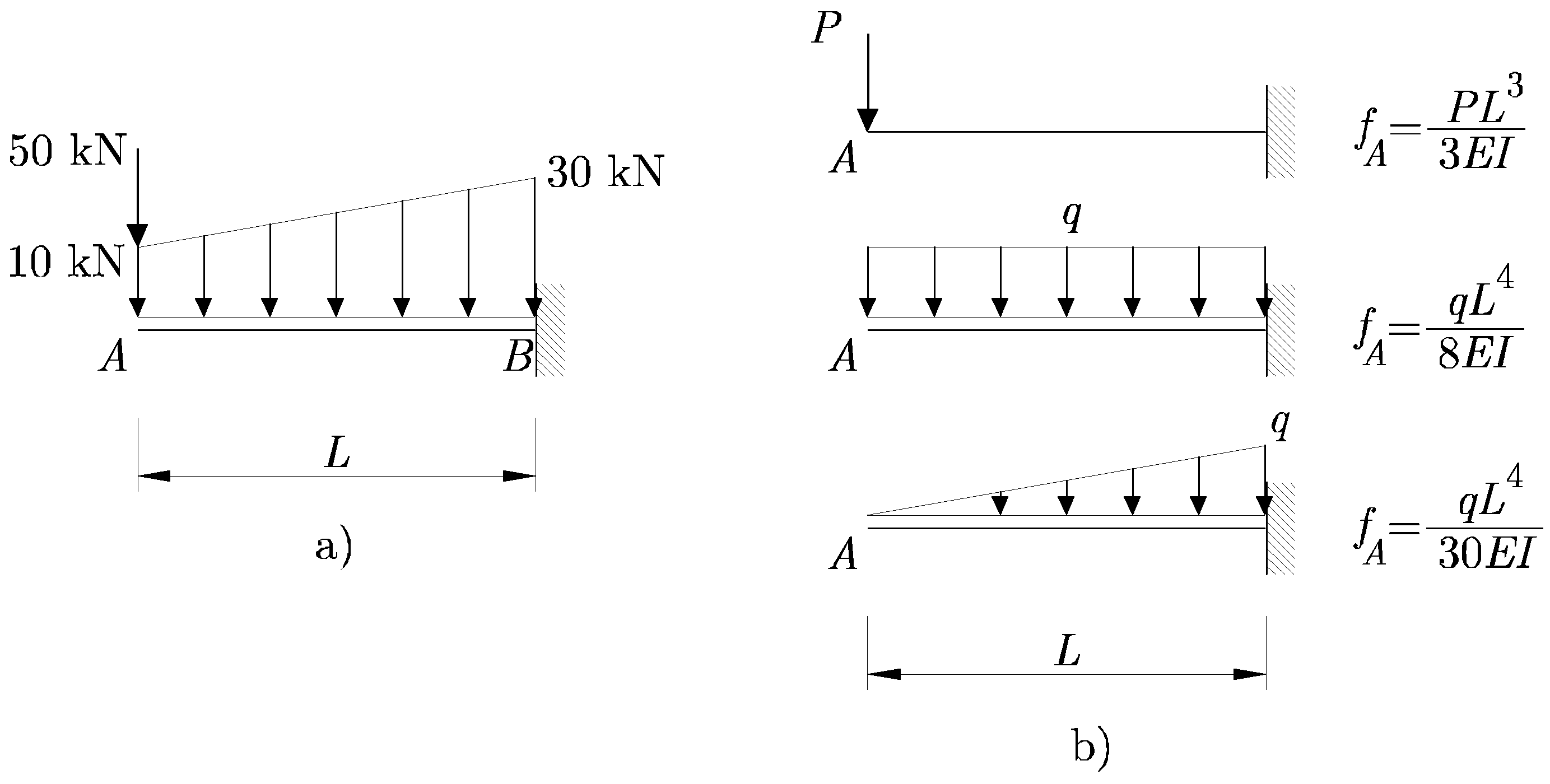 |
Obtener:
- El desplazamiento vertical del punto
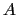 (
(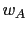 ), aplicando el principio de superposición
), aplicando el principio de superposición
Solución:
- Obtener el desplazamiento vertical del punto
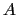 , aplicando el principio de superposición
, aplicando el principio de superposición
Ejercicio 3
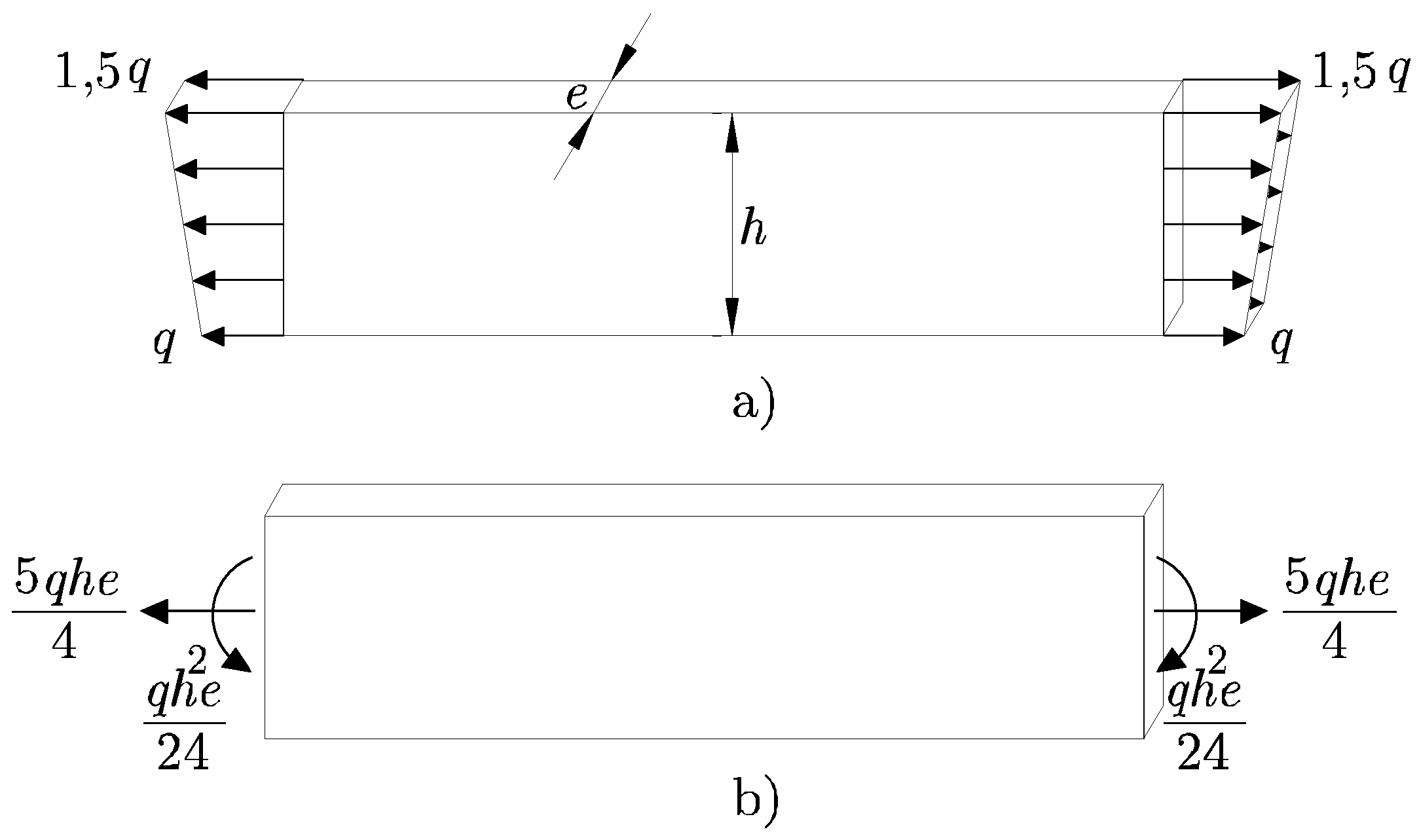
Para las placas cargadas que se muestran en la Figura 1.11,
Figura 1.11:
Aplicación del Principio de Saint-Venant
|
 |
Determinar:
- Si los sistemas de cargas aplicados en los extremos de las placas son estáticamente equivalentes
Solución:
- Determinar si los sistemas de cargas aplicados en los extremos de las placas son estáticamente equivalentes
- Fuerza resultante para el sistema de cargas que se muestra en la Figura 1.11 a):
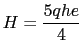
- Momento resultante para el sistema de cargas que se muestra en la Figura 1.11 a):
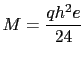
Por lo que sí son estáticamente equivalentes.