Torsión uniforme en barras prismáticas de sección no circular maciza

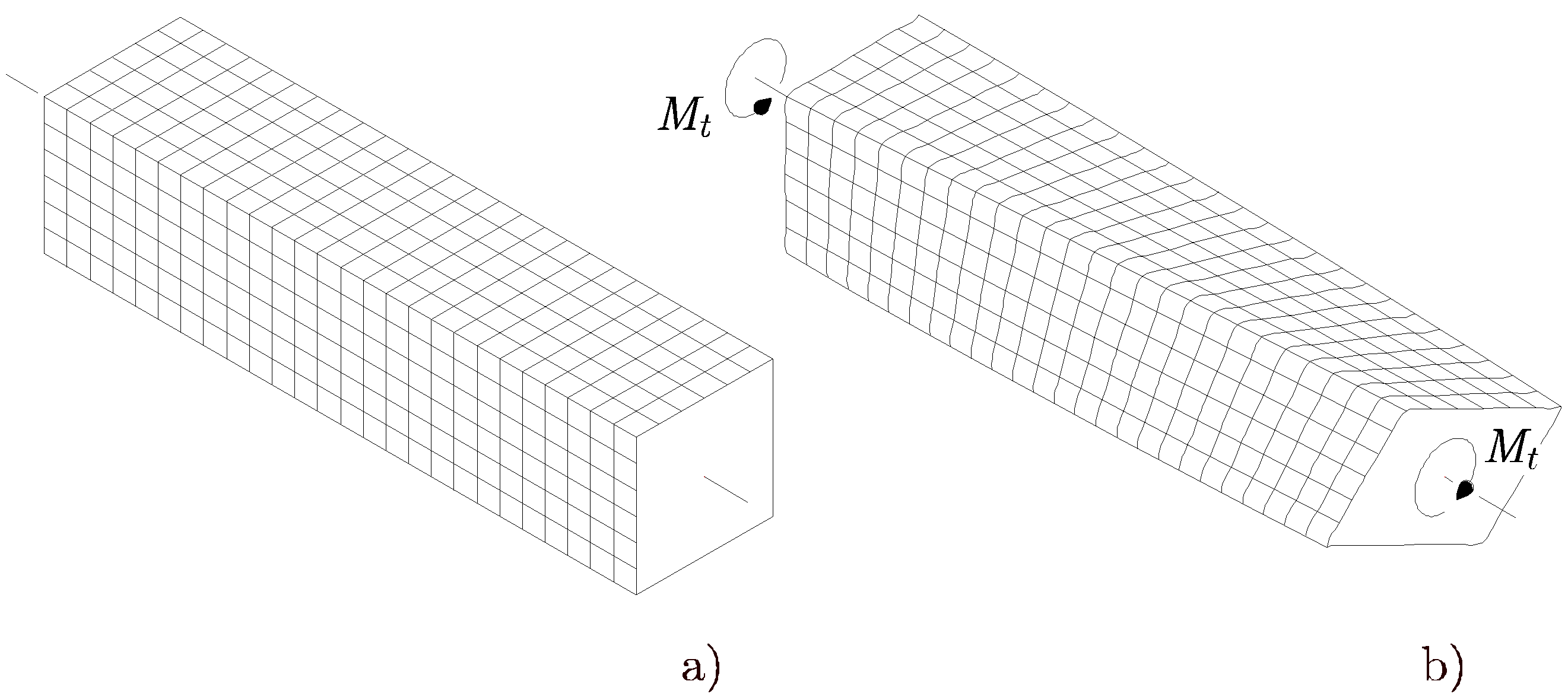
La Figura 11.4 muestra una barra prismática de sección transversal cuadrada sometida a torsión uniforme. Las secciones transversales planas normales al eje de la barra no permanecen planas durante la deformación (experimentan desplazamientos de alabeo) y sufren distorsión en su propio plano. Esto implica que no es posible establecer una teoría sencilla como la expuesta en el apartado 11.2.

Figura 11.4: Barra prismática de sección transversal cuadrada sometida a torsión
Image 4-torsion

Saint-Venant obtuvo la solución exacta al problema de torsión no uniforme en piezas prismáticas de forma arbitraria, suponiendo que la deformación es uniforme, y consiste en:

El problema debe ser formulado haciendo uso del modelo de medio continuo elástico.

L. Prandtl propuso en 1903 que las tensiones fueran expresadas a partir de una función de tensión $ \Phi\left(y,z\right)$, llamada también función de Prandtl, de forma que

$\displaystyle \tau_{xy}\left(x,y,z\right)=\displaystyle\frac{\partial \Phi \lef... ...ft(x,y,z\right)=\displaystyle\frac{-\partial \Phi \left(y,z\right)}{\partial y}$ (11.13)

El problema se reduce a encontrar una función $ \Phi\left(y,z\right)$ que satisfaga las ecuaciones de compatibilidad y las condiciones de contorno de la torsión uniforme. Esto implica que la función $ \Phi\left(y,z\right)$ satisfaga la ecuación diferencial

$\displaystyle \Delta \Phi\left(y,z\right)=\displaystyle\frac{\partial^2 \Phi\le... ...^2}+\displaystyle\frac{\partial^2 \Phi\left(y,z\right)}{\partial z^2}=-2G\theta$ (11.14)

con la condición de contorno de que la función de tensión sea constante a lo largo del contorno de la sección.

La resolución analítica de la torsión uniforme en barras prismáticas de sección no circular de sección maciza mediante el planteamiento del párrafo anterior es, en general, muy compleja. No obstante, se han obtenido distintas expresiones como solución a distintos tipos de secciones sometidas a torsión.