Fórmula de Cauchy. El tensor de tensiones

En el apartado 3.1 se afirmó que en un punto existen infinitos vectores tensión asociados a los infinitos planos que pasan por dicho punto. Surgía la pregunta de si existe alguna relación entre esos infinitos vectores tensión. Tal relación existe y viene dada por la fórmula de Cauchy.

Para deducir la fórmula de Cauchy, se parte de un tetraedro infinitesimal en el entorno de un punto $ P$. Tres de las caras son paralelas a los planos coordenados y se cortan en el punto $ P$, Figura 3.4 b), y la otra cara viene definida por un plano inclinado de normal $ \overrightarrow{n}$, Figura 3.4 a).

Figura 3.4: Tetraedro infinitesimal formado por a) caras paralelas a los planos coordenados y b) un plano de normal $ \overrightarrow{n}$
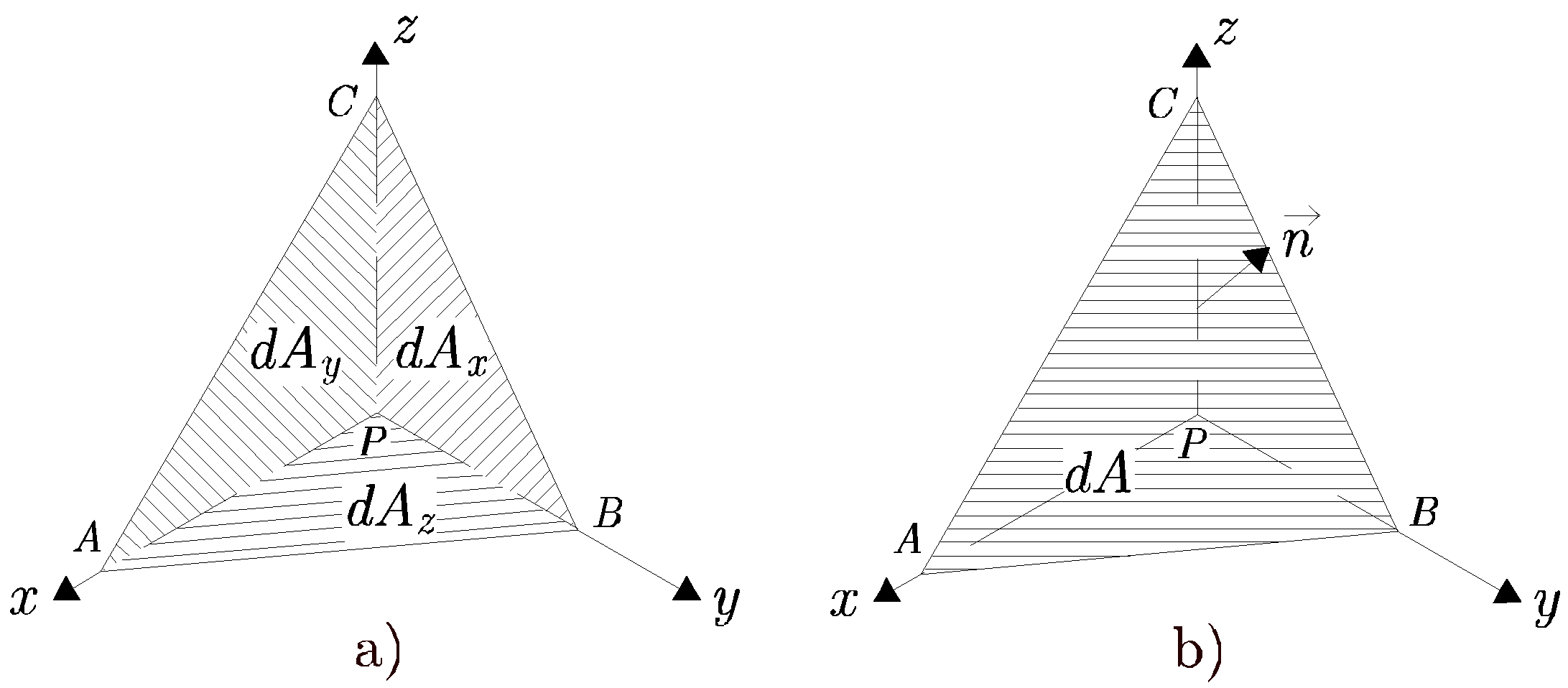Image 04-Tensiones

Si el área de la superficie de normal $ \overrightarrow{n}$ comprendida en el primer octante es $ dA$, las áreas de las otras tres superficies que forman el tetraedro serán


$\displaystyle dA_x$ $\displaystyle =$ $\displaystyle dA\cos\alpha=dA \hspace{1mm} l$  
$\displaystyle dA_y$ $\displaystyle =$ $\displaystyle dA\cos\beta=dA \hspace{1mm} m$ (3.5)
$\displaystyle dA_z$ $\displaystyle =$ $\displaystyle dA\cos\gamma=dA \hspace{1mm} n$  

siendo $ l$, $ m$ y $ n$ los cosenos directores de $ \overrightarrow{n}$.

Figura 3.5: a) Vector tensión sobre el plano de normal n b) Tensiones sobre las caras del tetraedro
Image 05-Tensiones

Estableciendo el equilibrio de fuerzas en dirección $ x$, Figuras 3.5 a) y b), se obtiene

$\displaystyle -\sigma_x \hspace{0.1cm}dA_x+\left(-\tau_{yx}\right)dA_y+\left(-\tau_{zx}\right)dA_z+t_x^n\hspace{0.1cm}dA +b_x \hspace{0.1cm} dV=0$ (3.6)

donde $ b_x$ es la componente en $ x$ de las fuerzas por unidad de volumen.

Sustituyendo las expresiones (3.5) en la ecuación (3.6), se obtiene

$\displaystyle -\sigma_x \hspace{0.1cm} dA \hspace{0.1cm} l +\left(-\tau_{yx}\ri... ...zx}\right)dA n \hspace{0.1cm} +t_x^n \hspace{0.1cm} dA +b_x \hspace{0.1cm} dV=0$ (3.7)

Dividiendo por $ dA$ y despreciando las fuerzas por unidad de volumen frente a las fuerzas por unidad de superficie, la ecuación de equilibrio de fuerzas en dirección $ x$, es

$\displaystyle \sigma_x l+\tau_{yx}m+\tau_{zx}n=t_x^n$ (3.8)

Planteando el equilibrio de fuerzas en las direcciones $ y$ y $ z$, se obtienen las ecuaciones

$\displaystyle \tau_{xy}l+\sigma_y m+\tau_{zy}n$ $\displaystyle =$ $\displaystyle t_y^n$ (3.9)
$\displaystyle \tau_{xz}l+\tau_{yz}m+\sigma_zn$ $\displaystyle =$ $\displaystyle t_z^n$ (3.10)

Estas tres ecuaciones se pueden expresar en forma matricial expandida como



$\displaystyle \left( \begin{array}{c} t_x^n \vspace{0.1cm}\\ t_y^n \vspace{... ...rray}{c} l \vspace{0.1cm}\\ m \vspace{0.1cm}\\ n \\ \end{array} \right)$ (3.11)



o bien, en forma matricial compacta

$\displaystyle \textbf{t}^{\text{\textbf{n}}}=\boldsymbol{\sigma} \text{\textbf{n}}$ (3.12)

A $ \boldsymbol{\sigma}$, que contiene los valores de las componentes de las tensiones en cada plano, se le denomina tensor de tensiones.

Las expresiones (3.11) y (3.12), indican que el vector tensión $ \overrightarrow{t^{\text{n}}} \left(\textbf{t}^{\text{\textbf{n}}}\right)$ correspondiente a un plano de normal $ \overrightarrow{n} \left(\textbf{n}\right)$ se obtiene multiplicando el tensor de tensiones por el vector unitario normal a dicho plano. Por consiguiente, el estado tensional en el interior de un sólido es conocido si lo es, en todos sus puntos, el tensor de tensiones.